Beaver lodges and burrows

Question

In the below diagram, A, B, C, D, E, F are beaver lodges and the segments in blue and red are burrows that connect the lodges. The dots marked with the letters G to S are crossing points where the beavers can change track. In the lodge A there are 3 beavers who want to reach their lodges in B, C and D. Obviously each beaver can follow several alternative paths to reach its lodge. According to the number of different paths that each beaver can follow, we will reward each with a corresponding number of apples. Each path consists of several burrows between the crossing points (the lodges in A to F can also be crossing points). A beaver can choose a specific burrow only if its ending crossing point is closer to its destination lodge, with respect to its point of origin. How many apples will each beaver gain?Lodges and burrows

It's really confusing; I can hardly understand the terms. Can anyone help?

For example, from A to B I think it is AB, AOB, ANOB, AOPB, ANOPB.

Answer 1

I'm attempting to solve for one of the beavers, just to see if I've figured it out :)

All in all, it is a graph traversal problem which you can solve with backtracking. I believe that he problem is NP complete, so you'll need an algorithm to count them all. I have implemented the graph and a depth-first search algorithm in python. It turns out that I was underestimating very much!

• Beaver 1: A$\to$B gets 5 apples
• Beaver 2: A$\to$C gets 41 apples
• Beaver 3: A$\to$D gets 121 apples Enjoy!

Python simulation

Import required packages

import numpy as np

Define the graph

nodes = {
  "A": [-np.sqrt(3)/2, -1/2], "B": [0,-1], "C": [np.sqrt(3)/2, -1/2], "D": [np.sqrt(3)/2, 1/2], "E": [0,1],
  "F": [-np.sqrt(3)/2, 1/2], "S": [1/np.sqrt(3),0], "J": [np.sqrt(3)/4, 1/4], "L": [-np.sqrt(3)/4, 1/4],
  "I": [1/(2*np.sqrt(3)) , 1/2], "K": [-np.sqrt(3)/4 , 1/4], "G": [-1/(2*np.sqrt(3)), 1/2], "H": [0, 1/2],
  "Q": [1/(2*np.sqrt(3)), -1/2], "N": [-np.sqrt(3)/4, -1/4], "M": [-1/np.sqrt(3),0], "P": [0, -1/2],
  "R": [np.sqrt(3)/4, -1/4], "O": [-1/(2*np.sqrt(3)), -1/2], "K": [0,0],
}

edges = [
  ["A","B"], ["A","O"], ["A",'N'], ['A','M'], ['A','F'], ['B','O'],
  ['B','P'], ['B','Q'], ['B','C'], ['C','Q'], ['C','R'], ['C','S'],
  ['C','D'], ['D','E'], ['D','S'], ['D','J'], ['D','I'], ['D','E'],
  ['E','I'], ['E','H'], ['E','G'], ['E','F'], ['F','G'], ['F','L'],
  ['F','M'], ['M','N'], ['N','O'], ['O','P'], ['P','Q'], ['Q','R'],
  ['R','S'], ['S','J'], ['J','I'], ['I','H'], ['H','G'], ['G','L'],
  ['L','M'], ['K','R'],  ['K','J'], ['K','H'], ['K','L'], ['K','N'],
  ['K','P'], 
]

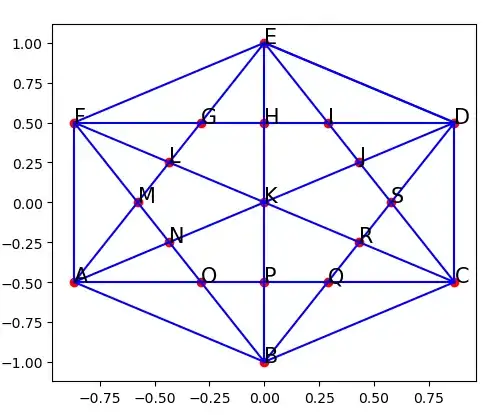
To test, here is a plot of the graph

for edge in edges:
  ls = nodes[edge[0]]
  le = nodes[edge[1]]
  plt.plot([ls[0], le[0]], [ls[1],le[1]], color="blue")

for p in nodes:
  l = nodes[p]

  plt.text(l[0],l[1],p)
  plt.scatter(l[0], l[1], color="red")

Auxiliary functions. The first one gets the other node in an edge; the second one computes the distance between two nodes.

def getOther(node, edge):
  a,b = edge
  if node == a:
    return b
  else:
    return a

def getDistance(node1, node2):
  x1,y1 = nodes[node1]
  x2,y2 = nodes[node2]

  return np.sqrt((x1 - x2)**2 + (y1- y2)**2)

Depth first graph search.

def getPaths(source, destination):
  pathsout = []
  stack = [source]
  while stack:
    path = stack.pop()
    node = path[-1]
    if node == destination:
      pathsout.append(path)

    dist = getDistance(node, destination)
    candidates = [getOther(node, edge) for edge in edges if node in edge]
    for c in candidates:
      if getDistance(c, destination) <= dist:
        stack.append(path + c )

  return set(pathsout) # transform into set to remove duplicates

Run simulation

print(f"n. paths from A to B: {len(getPaths('A','B'))}")
print(f"n. paths from A to C: {len(getPaths('A','C'))}")
print(f"n. paths from A to D: {len(getPaths('A','D'))}")

Results:

# paths from A to B: 5
# paths from A to C: 41
# paths from A to D: 121

Paths

Print are the paths the beavers can follow

print(f"n. paths from A to B: {len(getPaths('A','B'))}")
print(' '.join(getPaths('A','B')) + '\n\n')
print(f"n. paths from A to C: {len(getPaths('A','C'))}")
print(' '.join(getPaths('A','C')) + '\n\n')
print(f"n. paths from A to D: {len(getPaths('A','D'))}")
print(' '.join(getPaths('A','D')))

Results:

n. paths from A to B: 5
AOPB ANOPB ANOB AOB AB


n. paths from A to C: 41
ANKJSC ANOPQC AOBPQC AOBQRC ANOBQRC AMNOPQC AMNKJSC AOPQRC ANOPQRC AMNKPQC AMNKJSRC AOBC AMNOBC ABPQRC AMNKPQRC AMLKRC AMNKRC ANOBQC AOBQC ANKRC AOPQC ABQC AMNOBQC AMLKJSC AMNOPQRC ANOBPQRC ANKJSRC AMLKPQC AMLKJSRC AMNOBQRC AMNOBPQC ANOBC ABC AOBPQRC ANKPQRC ANOBPQC ABPQC AMLKPQRC AMNOBPQRC ANKPQC ABQRC


n. paths from A to D: 121
AOPKHID ABOPKHID AMNKRSD ABONKHID AMLGHID AFGHID AFMLGEID AMNKHID AONKRSJD AFMLGHID AFMLKHIJD AFGEHID AOPQCRSJD AFLGEID ABONKRSJD AMLKHIJD ABONKJD ABPQCSJD AMLKJD AFMLKHID AFLKJD ABOPKHIJD ABQCSD ABCSD AMLKRSD AOPKRSJD ABCD AONKRSD AFMNKRSD AFLGEIJD ABPKRSJD AMLGEHIJD AFGED ABOPQRSJD ABQCSJD AOPQCRSD AFGEHIJD ANKHIJD ABOPKRSD AOPQRSD AFMLGEHID AMLGED AMNKRSJD ABQRSD AMLKHID AFMLKJD AFLGED ANKRSD AFLKHIJD AFMLGED AONKHID ABPKJD AMLGEIJD AFGHIJD AMLKRSJD AFLGEHID ABPKHIJD ABPQCRSJD AMLGEHID AFEIJD ABONKHIJD ABONKRSD ANKJD AOPKHIJD ABPQCRSD AFGEIJD AFEHID AMLGEID ABPQCSD ABPQCD ABQRSJD AMLGHIJD ABPKHID ABCRSD ABPQRSJD ABCRSJD ABQCRSJD ABOPQCSJD AFMLGEIJD ABOPKJD AMNKHIJD AONKHIJD AMNKJD AFEID AFLGHID AFLKRSJD ANKHID ANKRSJD AFMNKJD AFED ABQCRSD ABOPQCRSJD ABOPQRSD AOPKRSD AFGEID AFLGHIJD ABQCD AOPQCSD AFMLKRSD AONKJD AFEHIJD ABCSJD AFMNKHID ABPKRSD AOPQCD AOPKJD ABOPKRSJD AFMNKRSJD ABOPQCD AFMLKRSJD AFMLGEHIJD ABPQRSD AFLGEHIJD AFMNKHIJD ABOPQCRSD AFMLGHIJD AOPQRSJD AOPQCSJD AFLKHID ABOPQCSD AFLKRSD