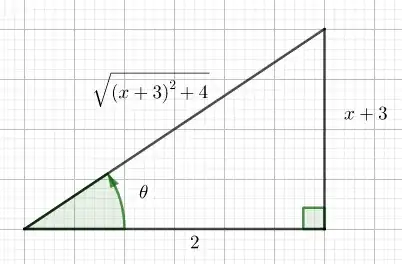
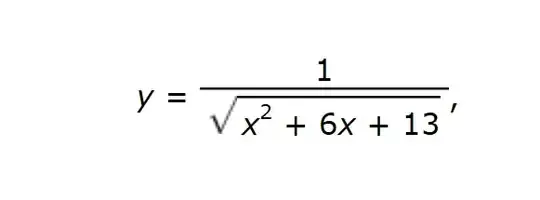Hi I am trying to solve an integral problem that involves trig substitution. First I tried completing the square, which gave me $1/\sqrt{(x+3)^2+2^2}$. I know I am supposed to use $x = \arctan(\theta)$. Does that mean it should be:
$x + 3 = \arctan(\theta)$
$x = \arctan(\theta) - 3$
and then Integrate from there? I am not sure if this is a good way of thinking about this problem. I would appreciate any help!
$$\int \frac{1}{\sqrt{x^2+6x+13}}\thinspace dx=\int\frac{1}{\sqrt{(x+3)^2+2^2}}\thinspace dx$$
So $x+3=2\tan\theta$, and $dx=2\sec^2\theta\thinspace d\theta$ \begin{eqnarray} \int\frac{1}{\sqrt{(x+3)^2+2^2}}\thinspace dx&=&=\frac{1}{2}\int\frac{2}{\sqrt{(x+3)^2+2^2}}\thinspace dx\\\ &=&\frac{1}{2}\int\cos(\theta)\sec^2(\theta)\thinspace d\theta\\\ &=&\frac{1}{2}\int\sec\theta\thinspace d\theta \end{eqnarray}
After completing the integration, substitute
$$\theta=\arctan\left(\frac{x+3}{2}\right)$$.
So you are trying to find $$I=\int\frac{dx}{\sqrt{x^2+6x+13}}=\int\frac{dx}{\sqrt{(x+3)^2+2^2}}$$ And your goal is to find the right substitution $$x+3=a\cdot\tan\theta$$ such that $$(x+3)^2+2^2=(a\tan\theta)^2+2^2=2^2(\tan^2\theta+1)=2^2\sec^2\theta.$$ It does not take much to show that $a=2$. Can you take it from here?
Do $x=2\tan(\theta)-3$ and $\mathrm dx=2\sec^2(\theta)\,\mathrm d\theta$. You will get$$\int\frac{2\sec^2(\theta)}{\sqrt{4\tan^2(\theta)+4}}\,\mathrm d\theta=\int\sec(\theta)\,\mathrm d\theta.$$Now, you can use the formula for the primitive of the secant.
Note that $$x^2+6x+13 = (x+3)^2+4$$
Your correct substitution is$$(x+3)=2\tan(\theta)$$
$$dx=2\sec^2(\theta)d\theta$$
$$(x+3)^2+4=4\tan ^2(\theta)+4 =4(1+\tan^2 (\theta)= 4\sec^2(\theta)$$
$$\sqrt {x^2+6x+13}=2\sec (\theta)$$
Will take care of the radical and the integral is manageable from here on.
