construct a quadrilateral with 4 given points as midpoints

Question

Given 4 points $P_1$, $P_2$, $P_3$, $P_4$ in the plane, is it always possible to construct a quadrilateral with these points as midpoints? With 3 points is very easy but I don't know how to proceed with four ...

Answer 1

No. The midpoints of the sides of a quadrilateral always form a parallellogram.

You can construct many quadrilaterals that lead to a given parallelogram. Essentially, you're free to pick any segment bisected by one of the four vertices. The rest is determined.

When you draw a picture you will probably choose a segment that lies outside the parallelogram, but that's not necessary. You can start with any single vertex and propagate that cyclically across vertices of the parallelogram using the parallelogram vertices as midpoints. Sometimes the resulting quadrilateral won't be convex. If your starting vertex is on the parallelogram the resulting quadrilateral is a triangle with an extra vertex on one side.

http://proofsfromthebook.com/2013/03/28/midpoints-of-quadrilateral/

Answer 2

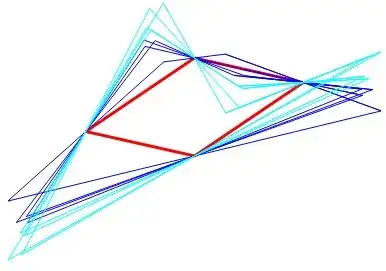
Fig. 1 : The given parallelogram (in red). Whatever the departure point $M$, once 4 central symmetries have been applied, one falls back on $M$. The generated parallelogram is convex (deep blue) iff "the vertices are in the regions bounded by three edges (extended) of the parallelogram" (thanks to @Ethan Bolker for this remark).

[One could generalize this problem to $n$ points ; in fact the case $n=4$ will help us to understand why the parity of $n$ plays a central rôle].

As pointed out by others, it is a necessary condition that the points form a parallegram. I will adress here the fact that there is an infinity of solutions, and even more, that any point in the plane can be chosen as one of the vertices of the parallelogram.

The easiest way to see it is by using the complex expression

$$z'=S_c(z)=2c-z\tag{1}$$

of central symmetry $z \to z'$ (with point $c$ as the center) ; (1) comes from constraint $c=\dfrac12(z+z').$

Let us consider the case $n=4$ : combining 4 central symmetries (see figure) :

$$T(z)=2c_4-(2c_3-(2c_2-(2c_1-z)))=2(c_4-c_3+c_2-c_1)+z\tag{2}$$

But a necessary and sufficient condition for $c_1,c_2,c_3,c_4$ to be the vertices of a parallelogram is precisely $(c_4-c_3)+(c_2-c_1)=0$. Thus, in such a case, (2) becomes $T(z)=z$ ; whatever the beginning point $z$, once the 4 central symmetries have been done, we are back at point $z$. There are an infinite number of solutions.

A similar situation will happen for all even values of $n$... Nothing similar exist for an odd value of $n$.

Maybe, later on, I will give an explanation of what happens when $n$ is odd and explain it with linear algebra tools (it becomes a kernel problem).

Answer 3

Here is a formula for five points. . The $Qi$ are $$P1+P2-P3+P4-P5,\\-P1+P2+P3-P4+P5,\\ P1-P2+P3+P4-P5,\\-P1+P2-P3+P4+P5,\\ P1-P2+P3-P4+P5$$