1

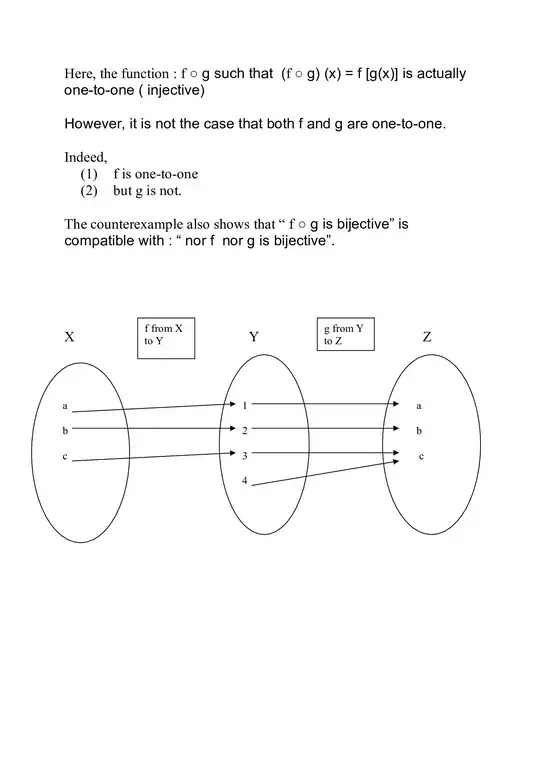
Suppose that $f:X\to Y$ and $g:Y\to Z$ are functions. If both $f$ and $g$ are one-to-one, then $g\circ f:X\to Z$ is one-to-one.

I believe the converse would be written: Suppose that $f:X\to Y$ and $g:Y\to Z$ are functions. If $g \circ f: X \to Z$ is one-to-one, then both $f$ and $g$ are one-to-one.

I cannot come up with a counterexample and I believe the converse is also true. Any thoughts.

Martin Sleziak
  • 53,687
user3753
  • 823
  • Counterexamples exist. To construct one, you could try and take $g$ to be something that is not one-to-one, but is one-to-one if restricted to the range of $f$. You can show though that $f$ must be one-to-one. – Minus One-Twelfth May 30 '19 at 13:53
  • https://math.stackexchange.com/a/76083/154545 – Surb May 31 '19 at 09:43
  • Please use a more descriptive title, and include background to your question: Why do you think this is true? What possible (counter)examples have you tried so far? – Jendrik Stelzner May 31 '19 at 09:48

3 Answers3

2

Take $g:\mathbb R\to \mathbb R$ defined by $g(x)=x^2$ and $f:\mathbb R^+\to \mathbb R$ defined by$f(x)=\sqrt x$. Then $g\circ f: \mathbb R^+\to \mathbb R$ is given by $(g\circ f)(x)=x$, that is injective, but $g$ is not injective.

Surb
  • 55,662
0

Let $X$ be a singleton.

Then automatically $g\circ f:X\to Z$ and $f:X\to Y$ are one-to-one.

But there are no restrictions for function $g:Y\to Z$ except that its domain $Y$ is not empty.

E.g. you can let $Y$ have at least two elements and take $g$ constant.

drhab
  • 151,093
0

Below a visual counterexample showing that the injectivity ( " one-to-oneness") of the composite function: f o g does not imply the injectivity of both f ang g.

It also shows that the bijectivity of f o g does not even imply f or g to be bijective.

In this counterexample, the composite function f o g is the identity function, but this need absolutely not be the case. In the setZ below ( see diagram) , substitute a for c, c for b and b for a, and you obtain a new f o g function that is not the identity function, but that is still one-to-one.

Note : making these substitutions in Z does not turn Z into a different set; for in a set as such there is no order, the "place" of elements does not count : {a, b c} = {c,a,b} = Z

enter image description here