The asymptotic behavior of $n\ln n -n$

Question

How do I show that $$\displaystyle\lim_{n\to\infty}\dfrac{n\ln n - n}{\ln n!}=1?$$

Answer 1

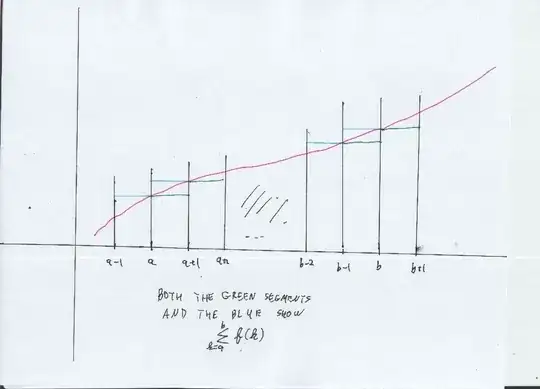
don't need Stirling. For a function such as logarithm with $f(x) > 0$ and $f'(x) > 0,$ we get $$ \int_{a-1}^b \; f(x) dx < \sum_{k=a}^b \; f(k) < \int_{a}^{b+1} \; f(x) dx $$

Here $f$ is log base e, take $a=2$ and $b=n$ $$ \int_{1}^n \; \log x \; dx < \sum_{k=2}^n \; \log k < \int_{2}^{n+1} \; \log x \; dx $$

An antiderivative of $\log x$ is $x \log x - x.$

$$ n \log n - n + 1 < \log n! < (n+1) \log (n+1) - n - 1 - 2 \log 2 + 2 $$

Answer 2

Using Stolz–Cesàro theorem you get $$\begin{align} \lim_{n\to\infty} \frac{n\ln n - n}{\ln n!} &= \lim_{n\to\infty} \frac{1 + (n+1)\ln(n+1) - n\ln n}{\ln (n+1)}\\ & = \lim_{n\to\infty} \frac{\ln(n+1) + n(\ln(n+1)-\ln n)}{\ln (n+1)} \\ &= \lim_{n\to\infty} \frac{\ln(n+1) + \ln\left(1+\frac1n\right)^{n}}{\ln (n+1)} \\ &= 1 \end{align}$$

You can also check some similar older questions (it seems natural that subtracting $n$ in the numerator does not change the limit):

• Limit of $\frac{\log(n!)}{n\log(n)}$ as $n\to\infty$. (one answer is based on Stolz Cesaro)
• How to calculate $\lim\limits_{x\to\infty} \frac{\log(x!)}{x\log(x)}$
• Calculate $\lim\limits_{n\to\infty}\frac{\ln(n!)}{n\ln(n)}$.
• Showing $\lim_{n \to +\infty} \log(n!)/(n\log n) = 1$ without using Stirling approximation (one answer using Stolz Cesaro)

Answer 3

Hint:

By Stirling' formula, $$\log n!\sim_\infty \log(2\pi n)+n\log n-n$$ so all you have to prove is that $$\frac{\log(2\pi n)}{n\log n-n}\to 0\quad\text{ as }\enspace n\to\infty.$$

Answer 4

As Bernard answered, the problem of the limit itself is quite simple using Stirling approximation of $\log(n!)$.

If you take one more term of this approximation, you could even get a quite good approximation since it will give $$\dfrac{n\ln n - n}{\ln n!}\sim 1-\frac{\ln (2 \pi n)}{2 n(\ln (n)-1)}$$ For example, using $n=100$, the exact value would be $0.991141$ while the approximation would give $0.991064$.