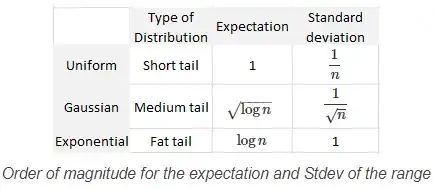
Here $X_1,\cdots,X_n$ are i.i.d. The two extremes $B=0$ and $B=2$, and the standard case $B = 1$ are illustrated in the picture below. For the reference, see here.
- 3,605
-
1What do you mean by variance of the range of $(X_1,..,X_n)$? – Kavi Rama Murthy May 25 '19 at 05:07
-
I mean $E[R_n^2] - E^2[R_n]$ with $R_n = \max(X_1,\cdots,X_n) - \min(X_1,\cdots,X_n)$. The distribution of the range depends on the distribution of the $X_k$'s, the general formula can be found at https://math.stackexchange.com/questions/3236430/recurrence-formula-for-the-moments-product-moments-of-some-order-statistics/3236452#3236452. – Vincent Granville May 25 '19 at 05:13
-
Asking a question in the title (only) is not a proper way to ask. As for the question, the expected value can be infinite, so the variance may be even undefined. Even if it is defined, it does not have to converge to zero. – zhoraster May 25 '19 at 06:51
-
Actually, in the exponential case, it does not converge to zero: the variance of the range converges to $\pi^2/(6\lambda^2)$, see the reference I provided. So $B=0$ and this case is covered. But of course, you need to exclude cases such as the Cauchy distribution, that don't have an expectation to start with. – Vincent Granville May 25 '19 at 07:42
-
1Regarding the standard Cauchy distribution, the range does not have an expectation, but it has a median (equal to 2 if $n=2$.) At first glance, it seems that the median of the range is $O(n)$ in this case. In general, the order of magnitude for the expectation of the range is $F^{-1}(n/(n+1)) - F^{-1}(1/(n+1))$ where $F$ is the cdf attached to the $X_k$'s. – Vincent Granville May 25 '19 at 08:49
-
If you had $f(x)=ke^{-x^\alpha}$ for $x \gt 0$, then what happens for $\alpha$ just above $0$? – Henry May 25 '19 at 09:04
1 Answers
Analysis of the range can be reduced to the analysis of extreme values attained by a distribution if it is bounded on one side. For such special cases, extreme value theory can be applied to study the behavior of the tail distributions/extreme order statistics. In particular, Fisher–Tippett–Gnedenko theorem can be applied under certain special structure of the underlying sampling distribution.
$\mathbb{VaR}[Range(X_1,X_2,...,X_n)]$ can be shown to be finite using Extreme Value Theory and convergence to generalized extreme value distributions.
Let $M_n = max(X_1,X_2,...,X_n)$ and $X_n$ follows a distribution bounded on the left. Then if there exists sequence of real numbers $a_n >0, b_n$ such that $\mathbb{Pr}(\frac{M_n -a_n}{b_n} < z) \to G(z)$, then G(z) follows a generalized extreme value (GEV) distribution. There are three possible GEV distribution Weibull, Gumbell and Fréchet distribution which are determined based on the convergence parameters $a_n,b_n$
Weibull, Gumbell distributions have finite variance and Fréchet distribution has finite variance if sampling distribution of $X_n$ has finite variance.
It can be shown that exponential distribution falls under the convergence law of Gumbell distribution with the same variance as mentioned in the comments. Polynomial tail distributions (heavier than exponential) fall under the convergence law of Fréchet distribution.
An example would be the Pareto distribution with polynomial tail which has CDF of,
$F_X(x) = 1 - (x_m/x)^{-\alpha}$ for $x \in [x_m,\infty)$ and $0$ otherwise
If $X_i \sim Pareto(\alpha)$ with $x_m = 1$, then $min(X_1,X_2,...,X_n)$ will converge to $x_m$ in probability as $n \to \infty$ and $Range(X_1,X_2,...,X_n)$ can be approximated as $max(X_1,X_2,...,X_n) - x_m$. Using the Fisher–Tippett–Gnedenko theorem, we can show that probability distribution of $M = \lim_{n \to \infty} max(X_1,X_2,...,X_n)$ converges to the Fréchet distribution with parameter $\alpha$.
The condition on $\alpha$ which makes variance of the Pareto distribution finite, also satisfies the condition to make the variance of the Fréchet distribution finite. Thus falling into the case where $B=0$.
I understand this answer doesn't capture all possible distributions of $X_n$ but the convergence criteria under Extreme Value Theory captures most of the heavy tail distributions used for modeling extreme observations.
- 405
-
I accepted the answer though it does not answer the full question, not explicitly. However, using EVT (extreme value theory) with the different types of limit distributions, as you suggested, definitely helps. Glad to see Pareto falling under $B=0$, that was my hope. Also, I don't think someone will post something more detailed. – Vincent Granville Jun 03 '19 at 18:05