I came across the following formulas for analytical expressions of fundamental modes of asymmetric dielectric waveguide. $$ \tan(x) = x\frac{\pi^2-x^2}{\pi^2-4x^2} $$ This approximation is not present in Abramowitz's handbook. It has the same poles and zeros as $\tan(x)$.
Can someone guide me on its merits or where to find it. This doesn't seem like an identity to me.
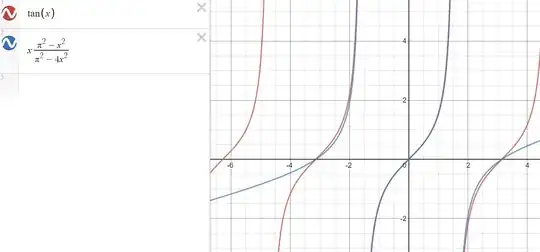
There are several ways to think about approximating $\tan x$ as a rational function.
Taking the log-derivative of $\sin x=x\prod_{k\ge 1}\left(1-\frac{x^2}{k^2\pi^2}\right)$ gives $$\cot x=\frac{1}{x}-2\sum_{k\ge 1}\frac{x}{k^2\pi^2-x^2}.$$Keeping only the $k=1$ term,$$\tan x\approx\frac{x(\pi^2-x^2)}{\pi^2-3x^2}.$$This is a reasonable approximation if $|x|\ll\pi$, so the right-hand side approximates$$x\left(1-\frac{x^2}{\pi^2}\right)\left(1+\frac{3x^2}{\pi^2}\right)\approx x+\frac{2}{\pi^2}x^3.$$However, the $3\mapsto 4$ replacement changes the $x^3$ coefficient to $\frac{3}{\pi^2}$, a much closer approximation of the exact result $\frac13$ (the Taylor series of $\tan x$ of course continues past the $x^3$ term).
A simpler motive for $\frac{\tan x}{x}\approx\frac{\pi^2-x^2}{\pi^2-4x^2}$ is that the right-hand side is an odd function and approximates $1$ for small $x$, diverges at $x=\pm\frac{\pi}{2}$ and vanishes at $x=\pm\pi$.
This is not an identity, but just an approximation for $\tan$.
If you look at their graphs, you'll notice that the two functions line up very, very well though for $|x|\leq\pi$.
As already said, this is an approximation.
In this domain, quite a lot of things can be done. Concerning the tangent, if you look here, you will see another one $$\tan(x) \sim x\frac{\pi^2 \left(\left(\frac{\pi ^2}{3}-\frac{17}{4}\right) x^2 +\pi^2\right) }{\left(x^2-4 \pi ^2\right) \left(x^2-\frac{\pi ^2}{4}\right)}$$ and notice that $\frac{\pi ^2}{3}-\frac{17}{4}$ is almost $-1$
