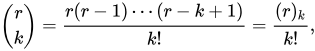Show that $\frac{x(x-1) \dots (x-n+1)}{n!} \in \mathbb{Z}$ with $x \in \mathbb{Z}$

Question

Problem: Let polynomial $Q_n (x) = \frac{x(x-1) \dots (x-n+1)}{n!} \in R[x]$ for some ring $R$. Show that $\forall t \in \mathbb{Z}, Q_n (t) \in \mathbb{Z}$.

My solution: For each $t \in \mathbb{Z}$, we have $t-1, t-2, \dots, t-n+1 \in \mathbb{Z}$, so $\frac{t(t-1) \dots (t-n+1)}{n!} \in \mathbb{Z}$ and $Q_n (t) \in \mathbb{Z}$.

Please check my solution. Thank all!

How do you know that each of the factors in the numerator is a multiple of one of the numbers from $1$ through $n$? — Aniruddha Deshmukh, May 22 '19 at 13:01
You have just stated that all factors in the numerator are integers. But instead, you should show that the numerator is a multiple of $n!$. To do this, you can read the answers here: The product of $n$ consecutive integers is divisible by $n$ factorial. — Minus One-Twelfth, May 22 '19 at 13:02
You proved nothing. The product of $n$ integers needn't be a multiple of $n!$. — , May 22 '19 at 13:02
The combinatorial argument: $Q_n(x)=\binom xn$ is the number of ways of choosing $n$ out of $x\ge n$ objects. For $0\le x<n$, one of the factors of the numerator is $0$. For $x<0$, the argument is similar to the one for $x\ge n$. — Shubham Johri, May 22 '19 at 13:03
I knew this formulate $\binom{m}{n} = \frac{n(n-1)\dots(n-m+1)}{m!}$. But with this formulate, the prove is clear. — Minh, May 22 '19 at 13:09

score 1 · Accepted Answer · answered May 22 '19 at 15:33

1

As shown here:

where $(\cdot )_{k}$ is the Pochhammer symbol, here standing for a falling factorial. So,
$$Q_n (x) = \frac{x(x-1) \dots (x-n+1)}{n!} = \frac {(x)_n} {n!} = \frac {\frac {x!} {(x-n)!}} {n!} = \frac {x!} {n! (x-n)!} = \binom x n \in R[x]$$ Now we know that $x$ is an integer so: $\forall t \in \mathbb{Z}, Q_n (t) \in \mathbb{Z}$.

answered May 22 '19 at 15:33

Anas Khaled

775

1

I know this formula but I cannot prove it – Minh May 22 '19 at 15:41

Show that $\frac{x(x-1) \dots (x-n+1)}{n!} \in \mathbb{Z}$ with $x \in \mathbb{Z}$

1 Answers1