1

Definition

Why is that the smallest positive element in the ideals of the form $a_1\mathbb Z + a_2\mathbb Z+...$ is the greatest common divisor of the coefficients $a_1, a_2...$?

I have seen a proof of that minimum positive element divides all of other elements without remainder but i can't understand how it can be the greatest common divisor. I can understand that any element in the ideal will be a multiple of the common divisors of the coefficients since we can factorize them to be so, but i can't see why it is the GCD. I am looking for intuition.

İbrahim İpek
  • 1,126
  • 1
    If $d$ is the minimal element of $I$, you seem to be happy that every element of the ideal is a multiple of $d$. Similarly, since $d$ is in $I$, every multiple of $d$ lies in $I$. So the elements of $I$ are exactly the multiples of $d$, and so

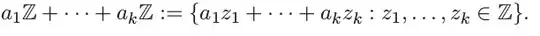
    $$I = (\ldots, -3d,-2d,-d,0,d,2d,3d,\ldots).$$

    But if this is true, then what is the GCD of the elements in $I$?

     – user670344 May 18 '19 at 15:20
  • 1
    It follows that $d=a_1z_1+\ldots +a_kz_k$ for suitable $z_i\in\Bbb Z$. Each summand on the right is a multiple of the $\gcd$, hence so is the sum, i.e., so is $d$. – Hagen von Eitzen May 18 '19 at 16:35
  • See here and here. – Bill Dubuque May 19 '19 at 04:01

1 Answers1

1

The GCD of the $a_i$s is a linear combination over $\mathbb{Z}$ of the $a_i$ from euclid GCD algorithm, hence $d\mathbb{Z}\subseteq I$, $I$ being your addition ideal $\sum_i a_i\mathbb{Z}$. Also, as $d\mid a_i\;\forall i$, we get $I\subseteq d\mathbb{Z}$. So, $I=d\mathbb{Z}$.

So, GCD is $d$, and it is the smallest linear combination as $d$ being generator of $I$ has to be the smallest element.

roydiptajit
  • 738