1

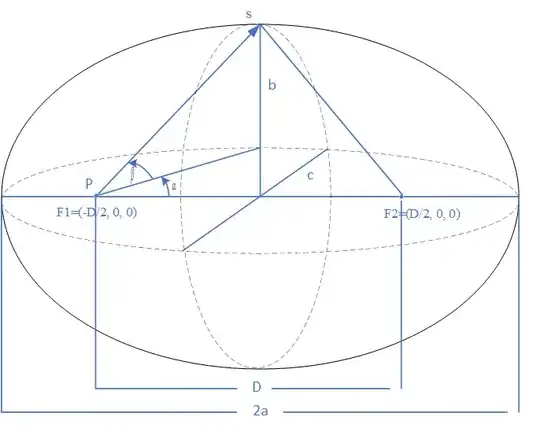
Given in $3D$ ellipsoid semi-major axis $a=5$, $b =4$ and $c=3$ . How can we find the distance $D$ between two focal points: $F_1$ and $F_2$? Also how can I find the distance from focal point $F_1$ or point $P$ to $S$ ? Will the distance from ($F_1 \rightarrow S$) + ($S \rightarrow F_2$) be equal to $2a$ like an ellipse ?

enter image description here

Álvaro Lozano-Robledo
  • 15,390
Urd Sher Qaisrani
  • 9
  • 4
    An ellipsoid doesn't have foci, in the sense that there aren't two points $F_1$ and $F_2$ such that the $|PF_1|+|PF_2|$ is constant for all points on the surface. (Adding more points to the sum doesn't help.) Note that, for an ellipsoid in "standard position", the coord planes cut an $ab$-ellipse (ie, one with radii $a$ and $b$), a $bc$-ellipse, and a $ca$-ellipse; each has its own foci and sum-of-distances property. Any plane through the center creates yet another ellipse. Now, your image seems to show $S$ and the $F_i$ in the $ab$-ellipse; for that ellipse, you can write $(d/2)^2=a^2-b^2$. – Blue May 10 '19 at 15:22

0 Answers0