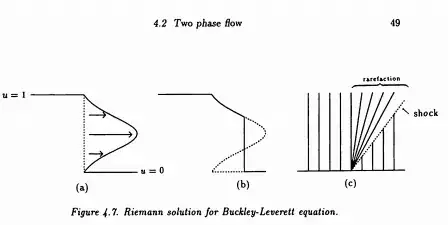
The same content is exposed in a section of Ref. (1) on the Buckley-Leverett equation as follows (p. 352-353):
We only need to solve for $q$, the water saturation, and so we can solve a scalar conservation law
$$ q_t + f(q)_x = 0 $$
with the flux $f(q)$ given by [
$$ f(q) = \frac{q^2}{q^2 + a (1-q)^2} . \tag{16.2} $$
Here $a<1$ is a constant]. Note that this flux is nonconvex, with a single inflection point.
and
Now consider the Riemann problem with initial states $q_l = 1$ and $q_r = 0$. By following characteristics, we can construct the triple-valued solution shown in [Fig. 4.7(a) of OP]. Note that the characteristic velocities are $f'(q)$, so that the profile of this bulge, seen here at time $t$, is simply the graph of $t f'(q)$ turned sideways.
Thus, we need to solve a Riemann problem in the nonconvex case. We consider a self-similar solution of the form $q(x,t) = v(\xi)$ with $\xi = x/t$. Using the chain rule, we have $q_t = v'(\xi)\xi_t$ and $q_x = v'(\xi)\xi_x$ with $\xi_t = -\xi/t$ and $\xi_x = 1/t$. Injecting the previous Ansatz in the quasi-linear PDE $q_t + f'(q)q_x = 0$ satisfied by the water saturation leads to
$$
\left(f'(v(\xi)) - \xi\right) {v'(\xi)} = 0\, ,
$$
which nontrivial solutions satisfy $f'(q(x,t)) = x/t$. Hence, the bulge at some time $t$ is obtained by plotting $x = t f'(q)$ for $q$ in $[0,1]$. This is illustrated below, where $a=1/2$ and $t=1$ (abscissas $q$, ordinates $x$):
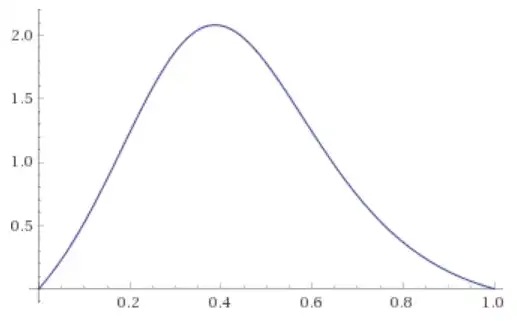
It remains to rotate the figure to obtain $q$ as a function of $x$. This topic is also well-explained in an interactive book, more precisely §1.6 and §5.1 on nonconvex conservation laws.
The equal area rule results from conservation, more precisely from the fact that a discontinuous weak solution must have the same integral as the smooth multivalued solution deduced from the characteristics. This is exactly the way it is applied in Fig. 4.7(b) of OP.
(1) R.J. LeVeque, Finite Volume Methods for Hyperbolic Problems, Cambridge University Press, 2002, doi:10.1017/CBO9780511791253