11

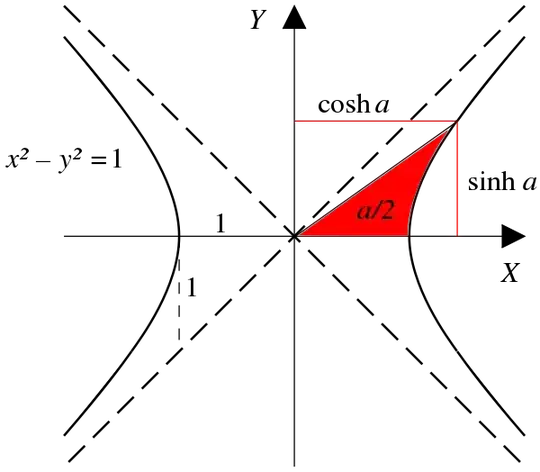
I am trying to understand geodesics and distance in hyperbolic space $H^n$ (Inverse image of $-1$ under $f(x_0,x_1,\dots,x_n)=-x_0^2+x_1^2+\dots+x_n^2$ and with the inherited metric). More precisely, I want to show that the Riemann distance between two points $p,q$ is $d(p,q)=arccosh(-p\cdot q)$.

Easy I thought, just compute the geodesics between two points $p,q$ and evaluate the length.

However, I don't really understand how to do this and would appreciate some help. How do I get a nice analytical formula which I can just "evaluate" to obtain the distance? In all the books I've read there are only very geometric arguments which don't really produce formulas and I don't really understand how to go between the two...

Elad
  • 3,137
afightingchance
  • 235

1 Answers1

10

I will write you a sketch. First start with geometric reasoning to determine the geodesics in the hyperboloid model of hyperbolic space.

  1. Let $O(1, n)$ denote the subgroup of linear transformations of $\mathbb{R}^{n+1}$ preserving the pseudo-Riemannian metric called the Lorentz metric $(\cdot, \cdot)$ of the . Let $O_+(1, n)$ denote the matrices $(a_{ij})_{i,j=0,\dots, n}$ in $O(1, n)$ with $a_{00} > 0$. Show that $O_+(1, n)$ is a subgroup of $O(1, n)$. Show that elements of $O_+(1, n)$ restrict to isometries of $H^n$.

    1. Determine the geodesics in the hyperboloid model of hyperbolic space: Let $P$ be a two-dimensional linear subspace of $\mathbb{R}^{n+1}$ containing the point $p \in H^n$. Show there is an element of $O_+(1, n)$ fixing $P$ and acting non-trivially on each point of $\mathbb{R}^{n+1}\backslash P$. Conclude that all geodesics of $H^n$ through $p$ can be obtained as intersections $P \cap H^n$ for some $P$ as above. You will need to use: Let $(M,g)$ be a Riemannian and let $\varphi:M \to M$ be an isometry. Let $p \in M$ such that $$\varphi(p)=p$$ and let $v \in T_p M$ such that: $$d\varphi_p(v)=v$$ If $\gamma(t)=exp_p(tv)$ (the geodesic with velocity $v$ that start at $p$) then: $$\varphi \circ \gamma(t)=\gamma(t)$$ for all $t$. You will also use the fact that geodesic in a given deirection is unique.

    2. Klein disk model of hyperbolic space: Let $y_1,\dots, y_n$, be the standard coordinates on $D^n$. Equip $D^n$ with metric defined by $$g_{ij} = \frac{\delta_{ij}}{1-|y|^2}+\frac{y_i y_j}{(1-|y|^2)^2} $$

Define a map $h : H^n_1 \to D^n$ by $$y_i=\frac{x_i}{x_0}$$ Show that $h$ is an isometry.

  1. Show that the geodesics of part (2) are sent by $h$ to straight lines in the Klein model. (The map $h$ is a stereographic projection along lines through the origin, to $D^n \subset \{x_0 = 1\} \subset L^{n+1}$).The stereographic projection to the disk of a geodesic segment

  2. Now calculate the length of a straight line paramtized in arc length between the two points with the Klien metric.

This is not the fastest way to see this but it connects the geometric reasoning to a formula and you can understant the arrcosh function. Maybe now you will even be satisfied with the $arrcosh$ formula without the calculation. Because you can understand what we are measuring.
enter image description here

Elad
  • 3,137
  • An interesting side note, angles measured with respect to the Klein metric on the disk are not the same as with respect to the Euclidean metric on the disk. On the other hand, angles in the Poincare disk model are the same as in the Euclidean metric on the disk. Thus, we can portray angles (Poincare) or geodesics (Klein) intuitively, but not both. – Elad May 08 '19 at 11:44
  • Just wondering. If $P$ is the $x-y$ plane, would a rotation about the $z$-axis be considered as fixing $P$? – Diger Jan 30 '22 at 16:36
  • @Diger A rotation around the $z$ axis would not be considered as fixing $P$ even though it does fix $P$ setwise – Elad Feb 03 '22 at 13:18