Hopefully this not to frivolous to ask, I have wondered it for years. There is a strange pattern in the differences between various power.
For example if you square the numbers from one to ten the difference between each square is the odds numbers. Similar patterns exist in the powers through 6 (and I assume all of them).
I attached an example of what I mean. Does anyone know why this occurs. For each higher power the pattern moves one to the "right"
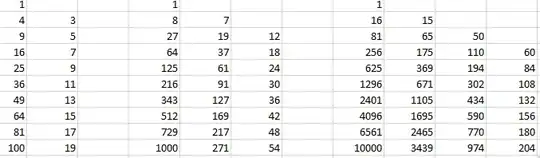
This is a well-known result analogous to the formula $$ \frac{d^k}{dx^k} x^k = k!$$for differentiation of polynomials. I'll try to state it clearly:
Definition: Let the discrete derivative of a sequence $a_1, a_2, a_3, \ldots$ be the sequence $a'_n := a_{n+1} - a_n$.
Remark: The discrete derivative is a linear operator. That is, if $c_n = \alpha a_n + \beta b_n$ for some constants $\alpha$ and $\beta$, then $c'_n = \alpha a'_n + \beta b'_n$.
Notation: Iterated discrete derivatives can be notated by parenthesized superscripts; thus $c^{(2)}$ for $c''$, $c^{(3)}$ for $c'''$, and so on.
Theorem: For some $k \geq 1$ fixed, let $a_n = n^k$ be the sequence of $k$th powers. Then $a_n^{(k)} = k!$ for all $n$.
Remark: An immediate consequence of this statement, used in a proof by induction, is that $a_n^{(\ell)} = 0$ if $k < \ell$.
Proof. The result is obvious for $k = 1$. Now assume that the result holds for all integers less than $k$. Then $$a'_n = (n+1)^k - n^k = k n^{k-1} + \binom{k}{2} n^{k-2} + \binom{k}{3} n^{k-3} + \cdots + kn + 1.$$
We know that $a_n^{(k)}$ is the $k-1$th discrete derivative of the RHS. Because the discrete derivative is a linear operator, we can take the derivative of each term on the RHS by itself. We know by the induction hypothesis that the $k-1$th derivative of $n^{k-1}$ is $(k-1)!$ and that the $k-1$th derivative of every other term in the RHS is zero, and we're done.
Note that the $k$th discrete derivative is a constant $k!$ for any polynomial with leading term $n^k$, not just the $k$th powers, as terms of smaller order drop out.
You are computing the finite differences of order $n-1$ of the $n^{th}$ powers of the integers.
Observe that by the binomial theorem, if we compute the first order difference of $m^n$ we have
$$(m+1)^n-m^n=nm^{n-1}+\frac{n(n-1)}2m^{n-2}+\cdots$$
Two important facts:
we started from a polynomial in $m$ of degree $n$, and obtained a polynomial of degree $n-1$;
the leading term has been multiplied by $n$.
If we iterate $n-1$ times, we obtain a polynomial of degree $1$ (linear) and the leading term has been multiplied by $n!$. Hence the general term is
$$n!m+c.$$
The $n^{th}$ column is the constant $n!$
The top values in every column have a closed form given here: https://oeis.org/A028246 (consider all subsequences starting with a $1$).
$$a(n,k) = \frac1k\sum_{i=0}^k (-1)^{k-i}\binom kii^n$$
Square numbers n*n are just the area of a square with side n. Notice how as you increase n (each side of the square) by one, you need an odd number of new squares.
These are the squares from $1^2$ to $5^2$ You can see that going from $4^2$ (orange) to $5^2$ (green) you need to add 9 squares. The same as 25 - 16.
If we have a polynomial $p(x)$ of degree $n$ with coefficients $a_i\in\mathbb{R}$ then we can write this as $$p(x)=a_0+a_1x+a_2x^2+\dots+a_nx^n$$ We can use the backward difference operator on this polynomial to get $$\nabla p(x)=p(x)-p(x-1)=\sum_{k=0}^n(a_kx^k-a_k(x-1)^k)$$ The resulting polynomial is always of degree one less than the intial polynomial which can be proven by noting that $$\begin{align} \sum_{k=0}^n(a_kx^k-a_k(x-1)^k) &=\sum_{k=0}^n(a_kx^k-a_k\sum_{j=0}^k\binom{k}{j}x^j(-1)^{k-j})\\ &=-a_k\sum_{j=0}^{k-1}\binom{k}{j}x^j(-1)^{k-j}+\sum_{k=0}^{n-1}(a_kx^k-a_k\sum_{j=0}^{k}\binom{k}{j}x^j(-1)^{k-j})\\ \end{align}$$ Hence this process can be repeated on the resulting polynomial which will once again reduce the degree by one. Eventually the polynomial degree is reduced to zero in which case each term is constant and equal to the difference between the terms in the previous polynomial.
In your case you have an initial polynomial of $$p(x)=x^k$$ for some $k\in\mathbb{N}$ and hence we can see that $$\nabla p(x)=x^k-(x-1)^k=x^k-\sum_{j=0}^k\binom{k}{j}x^j(-1)^{k-j}=kx^{k-1}-\frac{k(k-1)}2x^{k-2}+\dots$$ which means that this repeated process will both reduce the degree of the polynomial by one and multiply the highest power term of the polynomial by the highest power of the previous polynomial leaving a degree zero polynomial of $k(k-1)(k-2)\dots(1)=k!$ as a 'constant difference' between the corresponding degree one polynomial before it.
Another way to look at this is breaking down the operations: For squares:
You always need to add an odd number and an even number, each one higher than the last time, to get to the next square. For cubes, it is similar:
Always an odd number and two even numbers.
The 2nd iteration of cubes is:
Each time, you are adding the same three sides as the last 'layer' you added, plus the extra 'sides' (note these are
The extra 'sides' you add to the cube are each one bigger than the last time.
