0

What is wrong with my solution of the maximum value of $\displaystyle\sin \frac {A}{2} + \sin \frac{B}{2} + \sin \frac{C}{2}$ in a triangle ABC?

I am NOT after the answer.

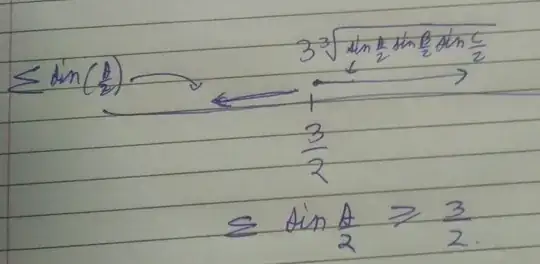
I know that $\displaystyle \sin \frac {A}{2}\sin \frac{B}{2}\sin \frac{C}{2} \leq 1/8 $

And I also know that arithmetic mean is greater than equal to the geometric mean.

$\displaystyle \sin \frac {A}{2} + \sin \frac{B}{2} + \sin \frac{C}{2} \geq 3[{\sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} }]^{1/3} $

$\displaystyle \sin \frac {A}{2} + \sin \frac{B}{2} + \sin \frac{C}{2} \geq 3/2 $

enter image description here

but this is wrong. Right is $ \sin \frac {A}{2} + \sin \frac{B}{2} + \sin \frac{C}{2} \leq 3/2 $

I am a high school student.

Michael Rozenberg
  • 194,933
user541396
  • 1,028
  • 8
  • 25
  • You know that the maximum for the geometric mean is $\dfrac{1}{2}$. But, consider the triangle where $A$ is very close to $\pi$ and $B$ and $C$ are both very close to zero. The geometric mean is very close to zero, but the arithmetic mean is very close to $1$. All you know is that the upper bound is $\ge \dfrac{3}{2}$. But, your argument does not tell you what that upper bound might be. It happens to also be $\dfrac{3}{2}$, but that is coincidence. Your argument tells you that $\dfrac{3}{2}$ is a lower bound for the upper bound of the arithmetic mean. – SlipEternal May 06 '19 at 15:24
  • @InterstellarProbe geometric mean would be 1/2 not 1/8. – user541396 May 06 '19 at 15:26
  • You are correct. But, my point still stands. – SlipEternal May 06 '19 at 15:27
  • @InterstellarProbe I am a high school student. I newer learned 'bounds'. Google search and wiki doesn't help me. It will be great if you could give me some source where I can study bound. Also 1/2 is still greater than 0 so what is the problem?? – user541396 May 06 '19 at 15:33
  • https://doubtnut.com/question-answer/in-triangle-a-b-c-prove-that-sina-2-sinb-2-sinc-2lt3-2dot-hence-deduce-that-cospi-a-4cospi-b-4cospi--22881?_gl=1kcktzh_ga*dEVPVWdPZDBFWG5jcXJZUlFCU0pwSGRmZ1ZDdE5BXzJpNzFVVFJJamxkMnc2X2lSUzFIZG5YaDVObU1lbElWcg.. – lab bhattacharjee May 06 '19 at 15:38
  • 1
    https://en.wikipedia.org/wiki/Upper_and_lower_bounds – SlipEternal May 06 '19 at 16:13

2 Answers2

1

Let $a,\,g$ respectively denote the half-angles' sines' arithmetic and geometric means. You know $g\le\frac12$ and $a\ge g$, but that doesn't imply $a\ge\frac12$, and (as you've clearly read somewhere) we can in fact prove $a\le\frac12$.

Let's first note an equaliteral triangle obtains $a=g=\sin\frac{\pi}{6}=\frac12$, and now let's see if we can prove $\sum_{i=1}^3\sin\frac{A_i}{2}$ cannot exceed this with $A_1:=A,\,A_2:=B,\,A_3:=C$. Since $0\lt\frac{A_i}{2}\lt\frac{\pi}{2}\implies\sin^{\prime\prime}\frac{A_i}{2}=-\sin\frac{A_i}{2}<0$, it suffices to use Jensen's inequality for concave functions (Eq. (2) here).

J.G.
  • 115,835
1

For $\alpha=\beta=\gamma$ we get a value $\frac{3}{2}.$

We'll prove that it's a maximal value.

Indeed, in the standard notation by AM-GM we obtain: $$\sum_{cyc}\sin\frac{\alpha}{2}=\sum_{cyc}\sqrt{\frac{1-\frac{b^2+c^2-a^2}{2bc}}{2}}=\frac{1}{2}\sum_{cyc}\sqrt{\frac{(a+b-c)(a+c-b)}{bc}}\leq$$ $$\leq\frac{1}{4}\sum_{cyc}\left(\frac{a+b-c}{b}+\frac{a+c-b}{c}\right)=\frac{1}{4}\sum_{cyc}\left(\frac{b+c-a}{c}+\frac{a+c-b}{c}\right)=\frac{3}{2}.$$

Michael Rozenberg
  • 194,933