0

Need help in vetting my answers for Q. 3,4,5 in section 2.2.2 in chap. 2 (page 7) in CRM series book by MAA: Exploratory Examples for Real Analysis, By Joanne E. Snow, Kirk E. Weller. Also, this post is in continuation of my last post's question. 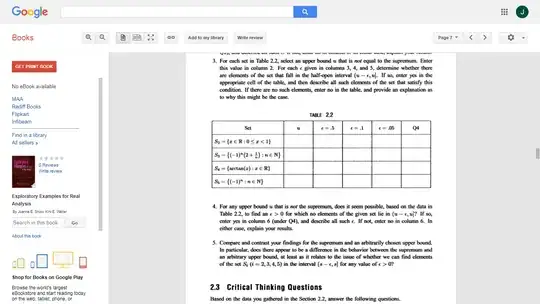here

3. For each set in Table 2.2, select an upper bound $u$ i.e. not equal to the supremum. Enter this value in column 2. For each $\epsilon$ given in columns 3,4, and 5, determine whether there are elements of the set that fall in the half-open interval $(u - \epsilon, u]$. If so, enter 'yes' in the appropriate cell of the table, & then describe all such elements of the set that satisfy this condition. If there are no such elements, enter ''no' in the table, & provide an explanation as to why this might be the case.

$$\begin{array}{c|c|c|c|c|} Set & \text{$u$} & \text{$\epsilon=.5$} & \text{$\epsilon=.1$} & \text{$\epsilon=.05$} & \text{$Q\, 4$} \\ \hline S_2 = \{x\in \mathbb{R}: 0\le x \lt 1 \} & 1.001 & (.501,1] & (0.901,1] & (0.951,1] & Yes \\ & & & & &(\forall u | u-s \ge \epsilon) \\ \hline S_3 = \{(-1)^n(2+\frac 1n)\,: n\in \mathbb{N}\} & 2.51 & \{2.01,\cdots,2.5\} & \{2.5\} & \{2.5\} & --do--\\ \hline S_4 = \{arctan(x)\,: x\in \mathbb{R}\} & \frac \pi{2} + 0.1 & (\frac \pi{2} - 0.4, \frac \pi{2}) & no & no & --do-- \\ \hline S_5 = \{(-1)^n\,: n\in \mathbb{N}\} & 1.2 & \{1\} & no & no & --do-- \\ \hline \end{array}$$

The columns under $\epsilon=0.5, 0.1, 0.05$ headings are found below:

$S_2 = \{x\in \mathbb{R}: 0\le x \lt 1 \} $ : $s=1$, let $u=1.001$.

>$\epsilon=.5$ : Desired interval is $(.501,1.001]$. The elements of set $S_1$ in interval are in $(.501,1.001]\cap S_1 = (.501,1)$.

>$\epsilon=.1$ : Desired interval is $(.901,1.001]$. The elements of set $S_1$ in interval are in $(.901,1.001]\cap S_1 = (.901,1)$.

>$\epsilon=.05$ : Desired interval is $(.951,1.001]$. The elements of set $S_1$ in interval are in $(.951,1.001]\cap S_1 = (.951,1)$.

$S_3 = \{(-1)^n(2+\frac 1n)\,: n\in \mathbb{N}\}$ : $s=2.5$, let $u = 2.51$.

As shown in my last post, $S_3=\{-3,-2.\overline{33},-2.2, -2.\overline{2.142857}, -2.\overline{1}, \cdots,2.25,2.1\overline{6},2.125,2.5\}$.
>$\epsilon=.5$ : Want to obtain the first term in the series for which get value $\ge 2.01$. Will check if get an element of the $S_3$ at the lower bound of the interval.

$2.01 = 2 + \frac 1n\implies .01n=1\implies n = 100$
Putting $n=100$, in $(-1)^n(2+\frac 1n)$ get $(-1)^{100}(2+\frac 1{100})\implies \frac {201}{100}= 2.01$.
Hence, the set is having element at the lower bound, but not included as open bound there.

>$\epsilon=.1$ : Want to obtain the first term in the series for which get value $\ge 2.41$.

$2.41 = 2 + \frac 1n\implies .41n=1\implies n = \frac{100}{41} \approx 2.43$.
Rounding off, get the nearest $n=2$.
$n=2$ is for supremum $=2.5 \gt 2.43$.
Hence, only one element $s$ is there.

>$\epsilon=.05$ : Want to obtain the first term in the series for which get value $\ge 2.46$.

$2.46 = 2 + \frac 1n\implies .46n=1\implies n = \frac{100}{46} \approx 2.17$.
Rounding off, get the nearest $n=2$.
$n=2$ is for supremum $=2.5 \gt 2.43$.
Hence, only one element $s$ is there.

$S_4 = \{arctan(x)\,: x\in \mathbb{R}\}$ :

Let, $u=\frac \pi{2} + 0.001$.
Note: The supremum value ($s$) is an irrational quantity. However, it is assumed to be attained for $x\rightarrow \infty$. For measurable values of $x$, $s$ is not attained.

>$\epsilon=.5$ : The range of interval is: $((\frac{\pi}2-0.4), \frac{\pi}2]$. The supremum is not in the range, but any value below $s$ should be. Also, taking $\tan((\frac \pi{2}+0.1) - 0.4 \approx 1.1707963267948966192313216916398)$ get measure as $49.49871336^o$. So, all reals in the interval $((\frac{\pi}2-0.4), \frac{\pi}2)$ are there.

>$\epsilon=.1$ : The range of interval is: $(\frac{\pi}2, \frac{\pi}2+0.1]$. Due to the supremum not being in the range, no element of set $S_4$ in the interval.
Note that $\epsilon (=.1)$ is the same as the difference between $u,s$, i.e. $u-s=0.1$.

>$\epsilon=.05$ : The range of interval is: $(\frac{\pi}2+0.1 -\epsilon (=.05), \frac{\pi}2+0.1]$. But, the lower bound is bigger than $s$, leading to no element of set $S_4$ in the interval.

$S_5 = \{(-1)^n\,: n\in \mathbb{N}\}$ :

$s = 1$, let $u=1.2$.

>$\epsilon=.5$ : The range of interval is: $(0.7, 2]$. The values of set in interval are $\{1\}$.

>$\epsilon=.1$ : The range of interval is: $(1.1, 2]$, i.e no values of set lie in interval.

>$\epsilon=.05$ : The range of interval is: $(1.05, 2]$, i.e no values of set lie in interval.

4. For any upper bound $u$ that is not the supremum, does it seem possible, based on the data in Table 2.2, to find an $\epsilon\gt 0$ for which no elements of the given set lie in $(u - \epsilon, u]$? If so, enter yes in column 6 (under $Q 2$) and describe all such $\epsilon$. If not, enter no in column 6. In either case, explain your results.

Yes, if $u-s \ge \epsilon$, then no element of set is in the desired interval, as even the supremum (even, if in range) will be not in the open lower bound.

5. Compare and contrast your findings for the supremum & an arbitrarily chosen upper bound. In particular, does there appear to be a difference in behavior between the supremum and an arbitrary chosen upper bound, as it relates to the issue of whether we can find elements of the set $S_i\,(i=2,3,4,5)$ in the interval $(s - \epsilon, s]$ for any value of $\epsilon \gt 0$?

The value of $\epsilon$ was not so important in the case of finding any element of the respective set $S_i\,(i=2,3,4,5)$ in the interval $(s-\epsilon, s]$, as $\epsilon\gt 0$; leading always to getting, at least some value, in the worst case of the supremum not being in the set & there being discrete values in range.
But, now need $u-s\lt \epsilon$ as a must to have any element in the sets in the interval $(u-\epsilon, u]$.

Let us consider all sets below for showing the latter case:

$S_2 = \{x\in \mathbb{R}: 0\le x \lt 1 \} $ :

If $u-s \ge \epsilon$, say as $s=1$, if $u=s+1, \epsilon=0.1$, then no element of $S_2$ is in the interval $(1.9,2]$.

$S_3 = \{(-1)^n(2+\frac 1n)\,: n\in \mathbb{N}\}$ :

As shown in my last post, $S_3=\{-3,-2.\overline{33},-2.2, -2.\overline{2.142857}, -2.\overline{1}, \cdots,2.25,2.1\overline{6},2.125,2.5\}$.
If $u-s \ge \epsilon$, say as $s=2.5$, if $u = 2.9, \epsilon = 0.1$, then no element of $S_3$ is in the interval.
Also, if $u-s \lt \epsilon$, say as $s=2.5$, then possible to have elements of the set in the interval. Say, if $u = 2.625, \epsilon = 0.5$, then the element of $S_3$ in the interval are in set $\{2.125,2.5\}$.

$S_4 = \{arctan(x)\,: x\in \mathbb{R}\}$ :

Let $u=\frac \pi{2} + k.\epsilon, k\gt 1$. Here, no value of set is in the interval $(\frac \pi{2} + (k-1).\epsilon, \frac \pi{2} + k.\epsilon]$.

$S_5 = \{(-1)^n\,: n\in \mathbb{N}\}$ :

Let $u=1+ k.\epsilon, k\gt 1$. Here, no value of set is in the interval $(1 + (k-1).\epsilon, 1+k.\epsilon]$.

Community
  • 1
jiten
  • 4,524

1 Answers1

1

  • Notice that $1 \notin S_2$, $(.501, 1.001] \cap S_2 = (0.501, 1).$

  • $S_3$ consists of discrete points, the intersection can't be an interval.

  • For question $4$, you might like to describe the set of $\epsilon$ explicitly.

Edit:

$$S_3 \cap (2.01, 2.51]=\{2+\frac1{2m}: 2+\frac1{2m}>2+\frac1{100}\}=\{2+\frac1{2m}: m< 50\}$$

Siong Thye Goh
  • 149,520
  • 20
  • 88
  • 149
  • Thanks, have edited for first two points. Please vet. But, the 3rd point is already implemented before & after the Q. 4, i.e. by taking $\epsilon$ values. So, feel for here, redundant. – jiten May 06 '19 at 17:06
  • Request to be in chatroom for Q. 2.4: 'Based on your answers to the prior questions, try to write "new" definition. This definition (let, Defn. 2) will involve a nonempty set $X$, a positive real $\epsilon$, & half-open interval $(s - \epsilon, s]$, where $s$ denotes supremum.' ---MY atempt is: A nonempty set $X$ will have its range $\cap(s - \epsilon, s]\ne \emptyset, ,, \forall \epsilon\gt 0$. ---But want to discuss my efforts at equivalence betn. conventional defn. (Defn. 1) & Defn. 2. Please chat https://chat.stackexchange.com/rooms/93126/discussion-between-siong-thye-goh-and-jiten. – jiten May 07 '19 at 06:34
  • Request elaboration of the selected answer in my post at : https://math.stackexchange.com/a/3217101/424260. Am unable to understand how to state an arbitrary set, i.e. bounded by defn.. I could not state there that it is part (b) of my earlier post at :https://math.stackexchange.com/q/3201755/424260. – jiten May 07 '19 at 12:46
  • Also, why your 'edit' here has chosen $\frac1{2m}$ rather than $\frac 1n$. Your choice might not work for odd values, say $101$. – jiten May 07 '19 at 12:55
  • 1
    because we know that odd terms are negative, which is not of our interest. – Siong Thye Goh May 07 '19 at 14:05
  • Please help in attempt on drawing equivalence betn. my new defn. (Defn. 2) of supremum (stated in my second comment) & usual lub based defn. (Defn.1). Need 2 sub-proofs: (a) given defn.1, arrive at defn. 2, (b) vice-versa. Attempt for (a) : Def. 1 implies: An upper bound $y\gt s$ will have set $X$ elements in $(y-\epsilon, y]$ if $y-s \lt \epsilon$. By proof: Let $y-s = k.\epsilon, 0\lt k\lt 1\implies y-s= k.\epsilon \implies y = s+k.\epsilon \implies y -\epsilon = s+(k-1).\epsilon \implies y-\epsilon \lt s$. New interval has even lower bound & higher upper bound in $(s+(k-1)\epsilon, y]$. – jiten May 07 '19 at 19:43
  • Please respond. Am eagerly waiting for a long time. – jiten May 07 '19 at 23:48
  • Have posted proof at : https://math.stackexchange.com/q/3217872/424260. Please help & vet. – jiten May 08 '19 at 01:59
  • 1
    Very busy day for me – Siong Thye Goh May 08 '19 at 02:41
  • Got no response for an much-effort-taking proof by me. If could spare some time, would be highly thankful. Else, would wait. – jiten May 08 '19 at 02:51