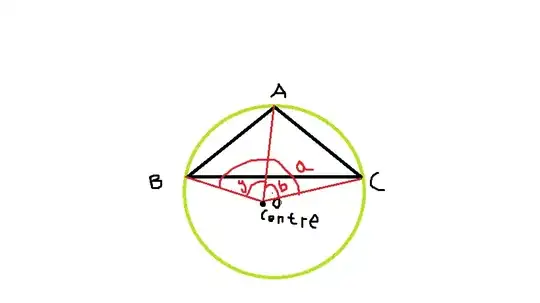
The side of a triangle inscribed in a given circle subtends angles $a, b, $ and $ y$ at the center.

Question

The side of a triangle inscribed in a given circle subtends angles $a, b,$ and $y$ at the center. The minimum value of the arithmetic mean mean of $ \cos (a+ \frac{\pi}{2}), \cos(b+\frac{\pi}{2})$ and $\cos(y+\frac{\pi}{2}) $ is . . . ?

One thing I noticed here is that either $a + b+y = 2 \pi $

or $a+y = b$ .

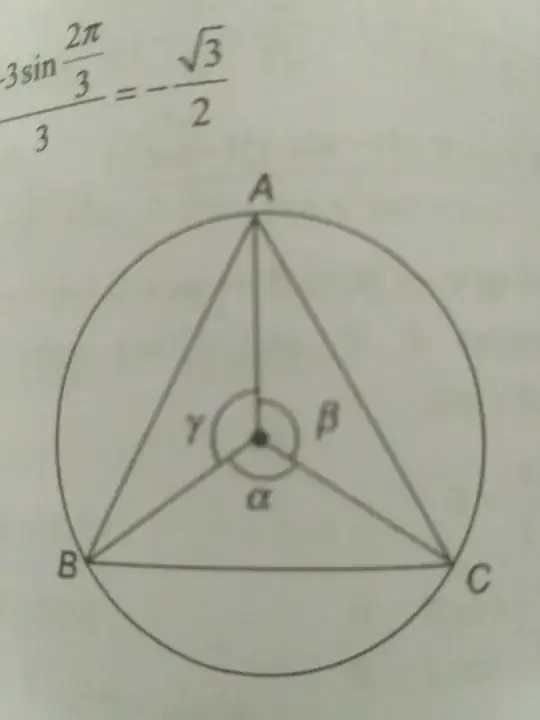
I used a diagram. I don't know if there is a more rigorous way to prove that. The problem can be solved if$ a + b + y = 2 \pi $ but what if it is the other case?

My book solve this problem using AM GM inequality but all these terms are negative so how can that be valid here , also they forgot the other case???

@Drmathva helped me solved it $ with a+b+c = 2 \pi$ case but what about the other case???

Answer 1

Case 1: $a+b+c=2\pi$

Observe, first of all, that we can expand $$\cos\big(a+\frac\pi2\big)=-\sin a$$

Thus, we want to maximize $$S=\sin a+\sin b+\sin c$$ under the constraint $a+b+c=2\pi$. Since we want to maximize $S$, we want all of it terms to be positive (this is not as rigorous as it might sound, so prove it!). Thus we can assume that $a,b,c\in (0,\pi)$. In that interval $$f(x)=\sin x\implies f''(x)=-\sin x<0$$ We now apply Jense's inequality $$\sin\bigg(\frac{a+b+c}{3}\bigg)=\frac{\sqrt 3}2\ge\frac{\sin a+\sin b+\sin c}3\iff S\le\frac{3\sqrt 3}2$$ Equality holds iff $a=b=c=\frac{2\pi}3$

---

Addendum

The second case doesn't really exist

In fact, we didn't consider the angle subtended by $\color{fuchsia}c$ correctly! And we are done!

---

Addendum 2

Please observe that the proof given by your book is wrong!

Consider for instance $f(x):=x+3$. With the same argument given by your book, $f(x)_{min}$ in $(0, \infty)$ is achieved when $x=3$. But this is wrong!

Of course $$x+3\ge 2\cdot \sqrt{3x}$$

and they are equal when $x=3$. But this doesn't imply that $x=3$ gives the minimum value for $f$...