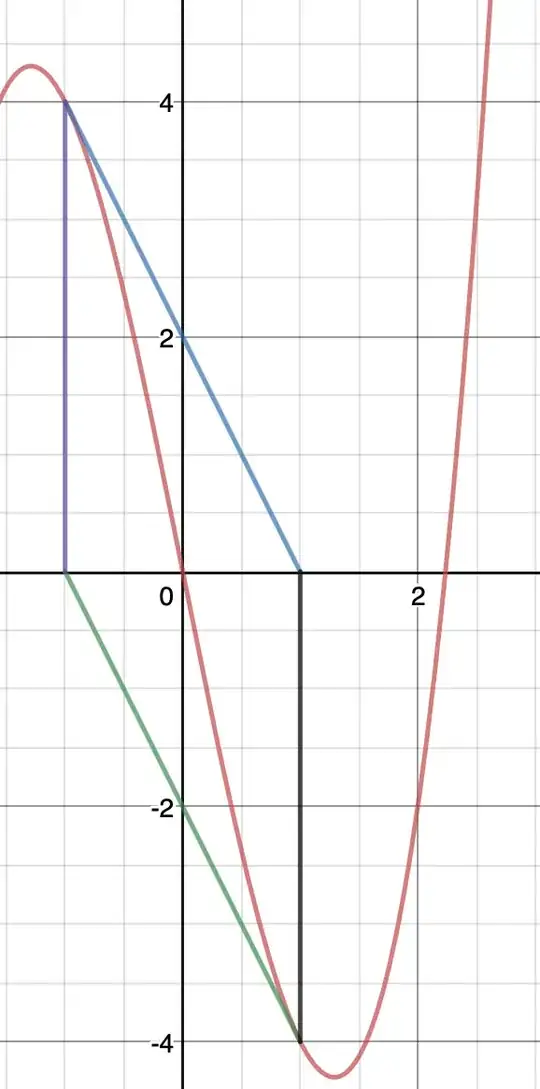
Apply Newton-Raphson method to find the solutions to the equation $x^3-5x=0$ starting with an initial guess of $x_0 = 1$.
While using Newton Raphson method, the value doesn't converge to a specific number. Rather, every iteration either gives $1$ or $-1$. Why does this happen? Any graphical interpretation for this?
For the graph of $f(x)=x^3-5x$, we have $f'(x)=3x^2-5$ $$f(1)=-4$$ $$f'(-1)=4$$ $$f'(1)=-2=f'(-1)$$
The tangent line at $x=1$ is $y+4=-2(x-1)$ which is $y=-2x-2$.
The tangent line at $x=-1$ is $y-4=-2(x+1)$ which is $y=-2x+2$
Geometrically, what has happened is you are trapped in the following cycle.
Starting from $(1,-4)$, by traveling along the tangent, we intercept the $x$-axis at $x=-1$. From $(-1,4)$, by trveling along the tangent, we intercept the $x$-axis at $x=1$.
The basic reason for this is that the graph of $f(x) = x^3 -5x$ has some symmetry. Specifically, $f(x)$ is an odd function.
The intuitive visualization of the Newton-Raphson method is that you are finding the tangent line to the curve at the initial guess point, and then finding the x-intercept of this line. You are then just repeating this, using the x-intercept you found as the next ‘guess’ point.
The first tangent line we find is given by $-2x -2$, which intersects the x-axis at $x=-1$, and because of the symmetry of the graph (the slope at $-x$ is the same as the slope at $x$), the tangent line here will intersect back at $x=1$. So we are stuck in a never-ending loop.
