1

When is $f=g$ on $(0,1)$ for

$f = \int_x^1y^{a-1}\left(1-y\right)^{b-1}dy$

$g = \left(2\frac{x+1}{x+2}\right)x^{a}\left(1-x\right)^{b-1}$

Let me show their graphs. They are small, so I multiplied it by 1000. How can I estimate those functions or find an answer explicitly? 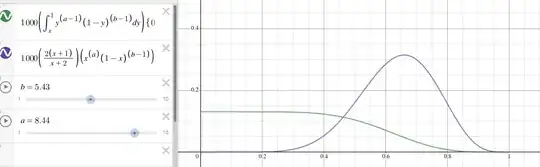screen of graphs UPD: as I move the sliders, I see, that they move the point of equality over curves that can be approximated by lines, but I am not very sure.

UPD2: I may be I can use another integral representation of Beta function, for example, $B(a,b) = 2 \int_0^{\frac{\pi}{2}} \cos^{2a-1}\theta \sin^{2b-1} \theta d\theta$, but that makes problem of defining incomplete Beta-function in this case, because integration bounds will be of type $acos(\theta)$. As discussed here, equation 15, polynomial representation is obtained from the representaton above putting $y = \cos^2\theta$.However, I don't see how that could help.

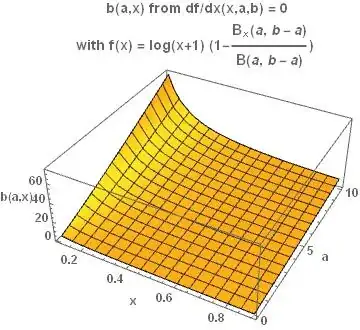
Background There was a question recently about finding maximum of

$$\log(1+x)\left( 1- \frac {\int_0^x t^{a-1} (1-t)^{b-a-1}dt}{B(a, b-a)}\right)$$

I tried to solve it.

I simplified it a bit, changed $(a, b-a)$ to $(a,b)$, As it's a product of two functions, and it has a clear maximum. I differentiated it.

$\Large{\frac{\left(\int_x^1y^{\left(a-1\right)}\left(1-y\right)^{\left(b-1\right)}dy\right)\ }{\left(\int_0^1y^{\left(a-1\right)}\left(1-y\right)^{\left(b-1\right)}dy\right)\left(1+x\right)\ }-\frac{\ln\left(1+x\right)\left(x^{\left(a-1\right)}\left(1-x\right)^{\left(b-1\right)}\right)}{\left(\int_0^1y^{\left(a-1\right)}\left(1-y\right)^{\left(b-1\right)}dy\right)}=0}$

Second: I used log representation to substitute $\ln(1+x)$ by $\frac{2x}{x+2}$ which is really good estimation of logarithm on $(0,1)$ interval

Lada Dudnikova
  • 1,359

2 Answers2

1

This is not a solution to the exact form of the OP but an extended comment which might be useful considering the additional information which was given in the OP.

Hence let us look at the maxima with respect to $x$ of the function defined in the "background" problem of the OP

$$f(x,a,b) = \log (x+1) \left(1-\frac{B_x(a,b-a)}{B(a,b-a)}\right)$$

After some tests I found that the overwiev of the position of the maximum can be obtained best inplicitly by the following graph. It shows the numerical solution

$$b(a,x)$$

of the equation

$$\frac{\partial}{\partial x} f(x,a,b) = 0$$.

It turns out that this form is favourable over the solution with respect to the natural variable $x$ because the solution procedure is stable.

enter image description here

This looks rather simple and can be described as follows: the dependence of $b$ on $a$ for given $x$ is roughly linear

$$b(x,a) = A(x) + B(x) a$$

the coefficients $A$ and $B$ depend on $x$ in a manner that can be seen in the graph.

For the precise determination of maxima in practical cases I suggest the same implicit numerical approach.

For information I provide the plot command in Mathematica which includes the root finding command.

An equivalent but more convenient form of $f'(x)$ is defined as $g1$ 

g1[x_, a_, b_] = 
 Beta[a, -a + b] - 
  Beta[x, a, -a + b] - (1 - x)^(-1 - a + b)
    x^(-1 + a) (1 + x) Log[1 + x]

and this is plotted with

 Plot3D[b /. FindRoot[g1[x, a, b] == 0, {b, a + 0.1}], {x, 0.1, 
  0.9}, {a, 0, 10}]
Dr. Wolfgang Hintze
  • 12,465
0

I suggest you use a numerical method. If you look for the first and second derivative of $f-g$, you can use the newton-raphson method, which converges really fast to a solution. Another effective and efficient method is the secant method. Both can be easily performed in Python:

  def secant(f,a,b,N):
'''Approximate solution of f(x)=0 on interval [a,b] by the secant method.

Parameters
----------
f : function
    The function for which we are trying to approximate a solution f(x)=0.
a,b : numbers
    The interval in which to search for a solution. The function returns
    None if f(a)*f(b) >= 0 since a solution is not guaranteed.
N : (positive) integer
    The number of iterations to implement.

Returns
-------
m_N : number
    The x intercept of the secant line on the the Nth interval
        m_n = a_n - f(a_n)*(b_n - a_n)/(f(b_n) - f(a_n))
    The initial interval [a_0,b_0] is given by [a,b]. If f(m_n) == 0
    for some intercept m_n then the function returns this solution.
    If all signs of values f(a_n), f(b_n) and f(m_n) are the same at any
    iterations, the secant method fails and return None.

Examples
--------
>>> f = lambda x: x**2 - x - 1
>>> secant(f,1,2,5)
1.6180257510729614
'''
if f(a)*f(b) >= 0:
    print("Secant method fails.")
    return None
a_n = a
b_n = b
for n in range(1,N+1):
    m_n = a_n - f(a_n)*(b_n - a_n)/(f(b_n) - f(a_n))
    f_m_n = f(m_n)
    if f(a_n)*f_m_n < 0:
        a_n = a_n
        b_n = m_n
    elif f(b_n)*f_m_n < 0:
        a_n = m_n
        b_n = b_n
    elif f_m_n == 0:
        print("Found exact solution.")
        return m_n
    else:
        print("Secant method fails.")
        return None
return a_n - f(a_n)*(b_n - a_n)/(f(b_n) - f(a_n))



approx = secant(f = lambda x: $f-g$,*value from where it needs to start 
searching*,*value from where it needs to end searching*,*times of repetition*)
print(approx)

Steven

Steven01123581321
  • 1,419