Number of paths on $\mathbb Z^d$

Question

Given two points $x,y \in \mathbb Z^d$ I am curious whether there is a formula for the number of paths $P(x,y,n)$ of length $n$(=number of steps) between $x$ and $y.$

Although an explicit expression would be nice, I am particularly curious to know if there exist sharp upper bounds on the scaling of $P(x,y,n)$ as a function of $n$. In particular, is it polynomial, exponential, factorial etc.?

So to be precise, the paths are allowed to be self-intersecting (and you can go back and forth,yes) and can move horizontically and vertically.

Please let me know if you have any questions.

Answer 1

Without loss of generality, let us assume that $y = (0,\dotsc, 0)$ is the origin. We write $x = (x_1, \dotsc, x_d)$.

Again without loss of generality, let us assume that every $x_i$ is non-negative. This is because we may "mirror" all the paths with respect to the $i$-th coordinate hyperplane.

We write $S$ for the sum of all $x_i$.

For the reason of parity, we should also assume that $n = 2m + S$ for some non-negative integer $m$, otherwise there is no such path.

With all these assumptions, the number of paths connecting $x$ and $y$, as function of $m$, is given by: $$f_d(m) = n!\sum_{a_1 + \dotsc + a_d = m}\frac{1}{\prod_{i = 1}^d\left(a_i!(a_i + x_i)!\right)}.$$

Reason: the number $a_i$ is the number of steps going in the negative direction of the $i$-th axis. Then we have to go $a_i + x_i$ steps in the positive direction of the $i$-th axis. The sum of all $a_i$ is just half of the steps that we "wasted", hence is equal to $m$; and once the numbers $a_i$ are all fixed, then we just choose how they are arranged in the total of $n$ steps, and there are $\frac{n!}{\prod_{i = 1}^d\left(a_i!(a_i + x_i)!\right)}$ such ways.

---

Example:

For $d = 1$, the function we have is simply $f_1(m) = \binom n m = \binom {2m + S} m$.

By Stirling, this is assymptotic to $\frac{2^{2m + S}}{\sqrt{\pi m}}$. (We say two functions $g(m)$ and $h(m)$ are assymptotic, or $f$ is assymptotic to $g$, if the limit $g(m)/h(m)$ tends to $1$ when $m$ tends to infinity.)

---

This paragraph has been edited. See the edit history for the previous version.

For $d = 2$, it turns out that there is again a closed formula.

We have \begin{eqnarray*} f_2(m) &=& n!\sum_{a_1 + a_2 = m}\frac{1}{a_1!a_2!(a_1 + x_1)!(a_2 + x_2)!}= \binom n m \sum_{a = 0}^m\binom m a \binom{m + S}{a + x_2}\\ &=& \binom n m \sum_{a = 0}^m\binom m a \binom{m + S}{m + x_1 - a} = \binom n m \binom n {m + x_1}. \end{eqnarray*}

Therefore, we have $f_2(m)$ assympotic to $\frac{2^{2n}}{\pi m}$, by Stirling.

---

This should give you a general taste of how $f_d$ grows with respect to $m$. More specifically, my feeling is that for every $d$ there exists a number $\alpha_d$ such that $f_d(m)$ grows "like" $\alpha_d^m$, up to some polynomial factor of $m$.

A trivial upper bound is $\alpha_d \leq 4d^2$, since every step has only $2d$ different choices, hence the total number of paths is $(2d)^n$, which is $(4d^2)^m$ up to constant factor. Thus a brave guess could be $\alpha_d = 2d$.

The idea of proof is to imitate the $d = 2$ case here. But to keep this answer in a reasonable length, I would like to pause the discussion here and leave it to interested people.

---

P.S. The problem obviously has an interpretation as random walks on lattices. So maybe there are probabilists who know this or are interested in this.

Answer 2

The best way to approach this is to instead consider a random walk on $\mathbb Z^d$ starting at the origin and ask for the probabilities that one ends at a specific point $z$ after $n$ steps. The reason for this is that we can define random variables $X_i$ for each step chosen uniformly from the $2d$ possible steps and then the ending position is just $X_1+\ldots + X_n$. These probabilities are just the quantities you want divided by $(2d)^n$, but thinking about it in these terms lets us bring in a powerful machine: the central limit theorem.

So, first of all, let's jump straight to the answer and come back to fill in the pesky details. Let $Z_n$ be a random variable given as the position after $n$ steps. The multivariate central limit theorem states that $$\frac{1}{\sqrt{n}}\cdot Z_n \rightarrow N\left(0,\frac{1}{d}\cdot I_n\right)$$ where $N$ is the multivariate normal distribution and $I_n$ is the identity matrix and the arrow means convergence in distribution. To unpack that with less jargon: the distribution of $\frac{1}{\sqrt{n}}\cdot Z_n$ tends to be the same as if we'd randomly chosen the coordinates, each from a normal distribution with variance $\frac{1}{d}$ - which is the variance of each $X_i$.

In particular, unless anything really bad happens, this means that the probability of being at a particular point $z$ after $n$ steps is roughly the probability of choosing, from the normal distribution, a point $p$ such that the closest point in $\frac{1}{\sqrt{n}}\mathbb Z^d$ with the correct parity is $\frac{1}{\sqrt{n}}z$. The probability density function of $N\left(0,\frac{1}d\cdot I_n\right)$ evaluated at $\frac{1}{\sqrt{n}}\cdot z$ is given as, where the product runs over all dimensions $$\prod_i \frac{\sqrt{d}}{\sqrt{2\pi}} \cdot \exp\left(-\frac{1}2\cdot \left(\frac{\sqrt{d}\cdot z_i}{\sqrt{n}}\right)^2\right) = \left(\frac{\sqrt{d}}{\sqrt{2\pi}}\right)^d\cdot \exp\left(-\frac{d\|z\|^2}{2n}\right).$$ The probability of this point being the closest point is roughly this evaluation of a PDF times the volume of the region in which $\frac{1}{\sqrt{n}}z$ is the closest point of the right parity - this volume being $2\left(\frac{1}{\sqrt{n}}\right)^d$, which gives the probability of ending at a $z$ of the right parity being roughly $$2\left(\frac{\sqrt{d}}{\sqrt{2\pi n}}\right)^d\cdot \exp\left(-\frac{d\|z\|^2}{2n}\right)$$ If we multiply this probability by the count of $(2d)^n$ equally likely paths of length of $n$, we get the following result:

The number of paths of length $n$ starting at the origin and ending at some point $z$ is approximately $$2(2d)^n\left(\frac{\sqrt{d}}{\sqrt{2\pi n}}\right)^d\cdot \exp\left(-\frac{d\|z\|^2}{2n}\right)$$

To be a bit more formal, all that we can use "convergence in distribution" to say is that if we choose some (measurable) region $A$ of $\mathbb R^d$ whose boundary has no $d$-volume, then the probability that $\frac{1}{\sqrt{n}}Z_n$ is in $A$ tends to, as $n$ goes to $\infty$, the probability that the same would happen for a normal distribution.

To use this at the origin, you can look at the probability that the ending position is within a ball of radius $\frac{\alpha}{\sqrt{n}}$ around the origin and have formally that this probability tends to be equal to the probability that the given normal distribution is within $\alpha$ of the origin. I'm struggling to recall a nice way to show this, but the probabilities of landing at any given point in this region are not too different from each other - essentially, the random walk doesn't remember where it started - so the probability of landing at a given point turns out to be really close to the total probability of the region divided by the number of points therein - which is also pretty much the asymptotic given before.

---

As mentioned by @Shalop in the comments, we can justify the asmyptotics on the probabilities of ending up at a given point by resorting to the use of some form of a local central limit theorem, which directly yield such results. For instance, Theorem 3 of this paper can be applied to this process after using a suitable change of coordinates to remove the parity issues.

One an also put together various ad-hoc approaches to prove this particular result, by noting that the probability of ending up at a particular point $z$ decreases in each coordinate of $z$'s absolute value, or that the ratio of adjacent probabilities can often be interpreted as events like "the probability of crossing a some hyperplane given that we ended up at some point" (which are very close to $1$) or that the differences of adjacent probabilities shrink quickly (which can be established via the Fourier methods in my other answer).

Answer 3

Here we give a combinatorial approach in terms of lattice paths for the special case of walks in a $d$-dimensional lattice which start and end at the origin. This problem is usually stated as Pólya's drunkard problem. Here we closely follow example VI.14 from Analytic Combinatorics by P. Flajolet and R. Sedgewick.

Pólya's drunkard problem: In the $d$-dimensional lattice path $\mathbb{Z}^d$ of points with integer coordinates, the drunkard performs a random walk starting from the origin with steps in $[-1,+1]^d$, each taken with equal likelihood. The probability that the drunkard is back at the origin after $2n$ steps is

\begin{align*} q_n^{(d)}=\left(\frac{1}{2^{2n}}\binom{2n}{n}\right)^d,\tag{1} \end{align*}

since the walk is a product of $d$ independent one-dimensional walks. The probability that $2n$ is the epoch of the first return to the origin is the quantity $p_n^{(d)}$,which is determined implicitly as results from the decomposition of loops into primitive loops by

\begin{align*} \left(1-\sum_{n=1}^\infty p_n^{(d)}z^n\right)^{-1}=\sum_{n=0}^\infty q_n^{(d)}z^n\tag{2} \end{align*}

In a previous section the authors define primitive loops as walks that start and end at the origin, but do not otherwise touch the origin. The generating function $\mathcal{L}$ of primitive loops is given as \begin{align*} \mathcal{L}(z)=1-\frac{1}{\sum_{n=0}^\infty \binom{2n}{n}^2z^{2n}}=4z^2+20z^4+176z^6+1876z^8+\cdots \end{align*} The coefficients are archived in OEIS as A054474. In particular $[z^{2n}]\mathcal{L}\left(\frac{z}{4}\right)$ is the probability that the random walk first returns to the origin in $2n$ steps.

In terms of the associated ordinary generating functions $P$ and $Q$, the relation (2) reads as $(1-P(z))^{-1}=Q(z)$, implying \begin{align*} P(z)=1-\frac{1}{Q(z)}\tag{3} \end{align*}

The asymptotic analysis of the $q_n$ can be done easily using Stirling's approximation of $n!\sim \left(\frac{n}{e}\right)^n\sqrt{2\pi n}$. In the following we give asymptotic expansions for the cases $d=1,d=2$ and $d=3$.

Case $d=1$:

This case can be solved directly from (1) and (3) by introducing \begin{align*} \beta(z)=\sum_{n\geq 0}\frac{1}{2^{2n}}\binom{2n}{n}z^n=\frac{1}{\sqrt{1-z}} \end{align*} With $P(z)=1-\sqrt{1-z}$ we obtain \begin{align*} \color{blue}{p_n^{(1)}}=\frac{1}{n2^{2n-1}}\binom{2n-2}{n-1}\color{blue}{\sim\frac{1}{2\sqrt{\pi n^3}}} \end{align*}

The cases $d>1$ can be solved by the Hadamard closure theorem. The Hadamard product of two functions $f(z)$ and $g(z)$ analytic at the origin is defined as their term-by-term product, \begin{align*} f(z)\odot g(z)=\sum_{n\geq 0}f_ng_nz^n\qquad\text{where}\qquad f(z)=\sum_{n\geq 0}f_nz^n,\quad g(z)=\sum_{n\geq 0}g_nz^n \end{align*} The Hadamard closure theorem (VI.11):

• (i) Assume that $f(z)$ and $g(z)$ are analytic in a $\triangle$-domain, $\triangle(\psi_{0},\eta)$ (see reference, figure VI.14 for more details). Then, the Hadamard product $(f\odot g)(z)$ is analytic in a (possibly smaller) $\triangle$-domain, $\triangle^{\prime}$.

• (ii) Assume further that \begin{align*} f(z)=O((1-z)^{\alpha})\quad \text{and}\quad g(z)=O((1-z)^b),\qquad z\in\triangle(\psi_0,\eta) \end{align*} Then the Hadamard product $(f\odot g)(z)$ admits in $\triangle^{\prime}$ an expansion given by the following rules (see reference, Theorem VI.11 for more rules):

  • If $a+b+1$ is a non-negative integer, then (with $\mathrm{L}(z)=\log(1-z)^{-1}$)

\begin{align*} (f\odot g)(z)=\sum_{j=0}^k\frac{(-1)^j}{j!}(f\odot g)^{(j)}(1)(1-z)^j+O\left((1-z)^{a+b+1}\mathrm{L}(z)\right). \end{align*}

Case $d=2$: By the Hadamard closure theorem, the function $Q(z)=\beta(z)\odot \beta(z)$ admits a priori a singular expansion at $z=1$ that is composed solely of elements of the form $(1-z)^{\alpha}$ possibly multiplied by integral powers of the logarithmic function $\mathrm{L}(z)=\log(1/(1-z))$.

The authors derive in the following an asymptotic expansion of $P(z)$ as

The singular expansion of $P(z)$ at $z=1$ results in \begin{align*} P(z)\sim 1-\frac{\pi}{\mathrm{L}(z)}+\frac{\pi^2 K}{\mathrm{L}(z)^2}+\cdots \end{align*} so that, by Theorems VI.2 and VI.3, one has \begin{align*} \color{blue}{p_n^{(2)}}&\color{blue}{=\frac{\pi}{n\log^2 n}-2\pi\frac{\gamma+\pi K}{n\log^3 n}+O\left(\frac{1}{n\log^4 n}\right)}\\ K&=1+\sum_{n=1}^\infty\left(16^{-n}\binom{2n}{n}^2-\frac{1}{\pi n}\right)\\ &\doteq 0.882\,542\,400\,610\,606\,373\,585\,825\,7\ldots \end{align*}

In a similar manner the authors also provide an expansion of the case $d=3$. Omitting some details we find

Case $d=3$: By singularity analysis the last expansion gives \begin{align*} \color{blue}{p_n^{(3)}}&\color{blue}{=\frac{1}{\pi^{3/2}Q(1)^2}\,\frac{1}{n^{3/2}}+O\left(\frac{1}{n^2}\right)}\\ Q(1)&=\frac{\pi}{\Gamma\left(\frac{3}{4}\right)^4}\\ &\doteq 1.393\,203\,929\,685\,676\,859\,184\,246\,3\ldots \end{align*}

The authors close this section with:

Higher dimensions are treated similarly, with logarithmic terms surfacing in asymptotic expansions for all even dimensions.

Note: Some further information regarding Pólya's drunkard problem is given in Pólya's Random Walk Constants.

---

---

Some related information regarding the general case is stated in section 5.9 Pólya's Random Walk Constants in Mathematical Constants by S.R. Finch.

From Pólya's Random Walk Constants (section 5.9):

• Let $U_{d,l,n}$ be the number of $d$-dimensional $n$-step walks that start from the origin and end at a lattice point $l$.

• Let $V_{d,l,n}$ be the number of $d$-dimensional $n$-step walks that start from the origin and reach the lattice point $l\ne 0$ for the first time at the end (second time if $l=0$).

Then the generating functions

\begin{align*} U_{d,l}(x)=\sum_{n=0}^\infty\frac{U_{d,l,n}}{(2d)^n}x^n,\quad V_{d,l}(x)=\sum_{n=0}^\infty\frac{V_{d,l,n}}{(2d)^n}x^n \end{align*}

satisfy

\begin{align*} V_{d,l}(x)&=\frac{U_{d,l}(x)}{U_{d,0}(x)}\qquad\qquad\quad l\ne 0\\ V_{d,0}(x)&=1-\frac{1}{U_{d,0}(x)} \end{align*}

Cases $d=1,d=2$:

\begin{align*} U_{1,l}(x)&=\sum_{n=0}^\infty\frac{1}{2^n}\binom{n}{\frac{l+n}{2}}x^n\\ U_{2,l}(x)&=\sum_{n=0}^\infty\frac{1}{4^n}\binom{n}{\frac{l_1+l_2+n}{2}}\binom{n}{\frac{l_1-l_2+n}{2}}x^n \end{align*}

where we agree to set the binomial coefficients equal to $0$ if $l+n$ is odd for $d=1$ or $l_1+l_2+n$ is odd for $d=2$.

Case $d=3$:

If $d=3$, then $a_n=U_{3,0,2n}$ satisfies according to the OEIS archived sequences A002896, A039699, A049037 and A063888:

\begin{align*} &a_n=\binom{2n}{n}\sum_{k=0}^n\binom{n}{k}^2\binom{2k}{k}=\sum_{k=0}^n\frac{(2n)!(2k)!}{(n-k)!^2k!^4}\\ &\sum_{n=0}^\infty\frac{a_n}{(2n)!}y^{2n}=I_0(2y)^3, \end{align*} where $I_0$ is the zero-th modified Bessel function and the $a_n$ fulfill the recurrence relation \begin{align*} (n+2)^3a_{n+2}-2(2n+3)(10n^2+30n+23)a_{n+1}+36(n+1)(2n+1)(2n+3)a_n=0. \end{align*}

Answer 4

While I was thinking about this, I came up with a second completely disjoint answer that gives an exact (but hard to evaluate) formula. We start by defining $P_n(z)$ to be the number of paths from the origin to $z$ of length $n$. One should notice that we know $P_1$ and can write $$P_{n+m}(z) = \sum_{a+b=z}P_n(a)P_m(b)$$ where the sum runs over all pairs $(a,b)$ that sum to $z$ in $\mathbb Z^d$. We can recognize that this formula can be rewritten in terms of convolution: $$P_{n+m}=P_n*P_m$$ where $f*g$ is the operation defined by $f*g(z) = \sum_{a+b=z}f(a)f(b)$. More directly, $P_n$ is a power in convolution: $$P_{n}=\underbrace{P_1*P_1*\ldots*P_1}_{n \text{ times}}.$$ This is great because we can invoke the Fourier transform in multiple dimensions (perhaps more properly known as an instance of Pontryagin duality) which transforms functions in such a way as to turn convolutions into multiplications - let me do this without invoking too much theory.

Let me start by doing this in a single dimension. Then $P_1(z)$ is a function that takes the value $1$ and $1$ and $-1$ and is $0$ everywhere else. We can rewrite this function as the following $$P_1(z)=\mathbb E[(a + a^{-1})\cdot a^z]$$ where $a$ is a variable chosen uniformly at random from the unit circle in $\mathbb C$. The coefficient $a+a^{-1}$ is usually called $\hat P_1(a)$ and the function $\hat P_1$ is the Fourier transform of $P_1$.

More explicitly, this means $$P_1(z)=\frac{1}{2\pi}\int_0^{2\pi}(e^{i\theta}+e^{-i\theta})\cdot e^{iz\theta}\,d\theta.$$ Note that $\int_0^{2\pi}e^{ai\theta}\,d\theta$ is $0$ when $a$ is a non-zero integer and $2\pi$ when $a=0$, so this whole integral only is non-zero when the $e^{iz\theta}$ terms cancel with either the $e^{i\theta}$ or $e^{-i\theta}$ terms. We can also work this out in only real terms to get $$P_1(z)=\frac{1}{2\pi}\int_0^{\pi}(e^{i\theta}+e^{-i\theta})\cdot (e^{iz\theta} + e^{-iz\theta}) = \frac{2}{\pi}\int_0^{\pi}\cos(\theta)\cos(z\theta).$$

However, we can use the theory of Fourier analysis note that $P_2=P_1*P_1$ is the same as saying $\hat P_2 = \hat P_1 \cdot \hat P_1$, which says that $$P_2(z) = \mathbb E[(a+a^{-1})^2\cdot a^z]$$ and since $(a+a^{-1})^2$ expands as $a^2+2+a^{-2}$, we can read off the number of paths to $2$ or $-2$ as the coefficients of $a^2$ and $a^{-2}$ respectively (1) and the number of paths ending at $0$ as the coefficient of $a^0$ (which is $2$). This is really the same as encoding everything in a generating function, but has a somewhat nicer language for our purposes. More generally $$P_n(z) = \mathbb E[(a+a^{-1})^n\cdot a^z]$$ which can be reduced down to the following real expression: $$P_n(z) = \frac{2^n}{\pi}\int_0^{\pi}\cos(\theta)^n\cdot \cos(z\theta)\,d\theta$$ from which we can derive asymptotics by noting that, for large $n$, the quantity $\cos(\theta)^n$ is close to zero except when one is close to $0$ or $\pi$. Let's leave this off until we have a general formula for all dimensions.

Doing a general expression isn't so hard; let's fix the dimension to be $d$ and write $P_n(z_1,\ldots,z_d)$ as the number of paths from $0$ to $(z_1,\ldots,z_d)$ with $n$ steps. One can, for similar reasons, verify that $$P_1(z_1,\ldots,z_d)=\mathbb E[(a_1+a_1^{-1}+a_2+a_2^{-1}+\ldots+a_d+a_d^{-1})\cdot a_1^{z_1}a_2^{z_2}\ldots a_d^{z_d}]$$ where each $a_i$ is randomly chosen from the unit circle. One merely has to verify that this gives $1$ when exactly one coordinate $z_i$ is $\pm 1$ - which is true for similar reasons to in the one dimensional case. Then, we get to write $$P_n(z_1,\ldots,z_d)=\mathbb E[(a_1+a_1^{-1}+a_2+a_2^{-1}+\ldots+a_d+a_d^{-1})^n\cdot a_1^{z_1}a_2^{z_2}\ldots a_d^{z_d}]$$ due to the convolutional formula - again, noting that if we expand the first term, we could read off the answers from there. Then, we can write this as an integral: $$P_n(z_1,\ldots,z_d)=\int_0^{2\pi}\ldots \int_{0}^{2\pi}(e^{i\theta_1} + e^{-i\theta_1} + \ldots + e^{i\theta_d} + e^{-i\theta_d})^n\cdot e^{iz_1\theta_1 + \ldots + iz_d\theta_d}\,d\theta_1 \ldots d\theta_d$$ which is clearly awful, but reduces to a real integral along similar lines to before: \begin{align*}P_n(z_1,\ldots,z_d)&=\frac{1}{(2\pi)^d}\int_0^{2\pi}\ldots \int_{0}^{2\pi}2^n(\cos(\theta_1) + \ldots +\cos(\theta_d))^n\cdot e^{iz_1\theta_1 + \ldots + iz_d\theta_d}\,d\theta_1 \ldots d\theta_d\\ &=\frac{(2d)^n}{(2\pi)^d}\int_0^{2\pi}\ldots \int_{0}^{2\pi}\left(\frac{\cos(\theta_1) + \ldots +\cos(\theta_d)}d\right)^n\cdot \cos(z_1\theta_1 + \ldots + z_d\theta_d)\,d\theta_1 \ldots d\theta_d\end{align*} Tada! This is a formula valid for all inputs and gives an exact result. Does it make it easier to evaluate the answer? Well, no - but it's more useful for deriving asymptotic results.

This integral, like the one dimensional one, is very concentrated around the points $(0,0,\ldots,0)$ (and its associates on the circle where every coordinate is among $0$ or $2\pi$)) and $(\pi,\pi,\ldots,\pi)$ since otherwise the term raised to the $n^{th}$ power will not be near $\pm 1$, hence will be small. At $(0,0,\ldots,0)$, the other term is $1$ and at $(\pi,\pi,\ldots,\pi)$, the other term is $1$ if the sum of the $z_i$ is even and $-1$ otherwise. This fact merely causes either doubling if the parity of this sum is the parity of $n$ or cancellation otherwise.

So, let's estimate that integral. In particular, let's try to estimate the integral of the term $\left(\frac{\cos(\theta_1) + \ldots +\cos(\theta_d)}d\right)^n$ near $\theta=(0,0,\ldots,0)$, noting that, for any small radius around $(0,0,\ldots,0)$, there is some $n$ large enough that the term will drop to arbitrarily small values outside of this radius (...until it gets to $(\pi,\pi,\ldots,\pi)$). In particular, we are justified by first estimating $\cos(\theta)$ by $1-\frac{1}2\theta^2$, since only small $\theta$ matter. Thus, a (very) good approximation to the integral is the integral of $$\left(1 - \frac{1}{2d}\left(\theta_1^2+\theta_2^2+\ldots+\theta_d^2\right)\right)^n$$ taken over the sphere the sum of those squares is at most $\frac{1}{2d}$ - i.e. a sphere of radius $\sqrt{\frac{1}{2d}}$. We can then group this integral by radius $r$ to get that that integral is equal to $$\int_0^{\sqrt{1/2d}} \left(1-\frac{r^2}{2d}\right)^n \cdot \frac{r^{d-1}d\pi^{d/2}}{\Gamma(1+\frac{d}2)}\,dr$$ where $\Gamma$ is the gamma function and $\frac{r^{d-1}d\pi^{d/2}}{\Gamma(1+\frac{d}2)}$ is the surface area of a $d$-dimensional sphere of radius $r$.

This integral is also pretty bad, but we can make our computer do it to get its value as $$\frac{(2\pi d)^{d/2}n!}{\Gamma(1+n+d/2)}.$$ We can immediately plug this in as an asymptotic for the number of paths from the origin to itself after an even number $n$ steps: $$P_n(0,0,\ldots,0) \approx 2\cdot \frac{(2d)^n}{(2\pi)^d}\cdot \frac{(2\pi d)^{d/2}n!}{\Gamma(1+n+d/2)}$$ One can also note that $\frac{n!}{\Gamma(1+n+d/2)}$ is a $O(n^{-d/2})$ term, so this, for fixed $d$, grows in $O\left(\frac{(2d)^n}{n^{d/2}}\right)$. Figuring out the constant term via this reasoning is left as an exercise to the reader - as is determining exactly what the order of this asymptotic is (it's quite close to the truth, but hard to quantify better than that. At the origin specifically, the previous display equation is a lower bound, since the only approximation we used at that point is $\cos(x) \approx 1 - x^2/2$ which is an underestimate).

One can also extend this to other $z$, but basically what this argument tells you is that, if $z$ is close enough to the origin (in relation to $\sqrt{n}$), that the term $\cos(z_1\theta_1+\ldots+z_n\theta_n)$ does not vary much from $1$ before the other term is negligible, the result is the same - in fact, the ratio of $\frac{P_{n}(z_1)}{P_n(0)}$ tends to $1$ in the limit as $n$ goes to $\infty$ for any fixed $z_1$. If $z$ is really far from the origin, then this term oscillates in the regions where the other term is significant, hence causes cancellations - you could, of course, use the same approximation, but keeping the final term, and it's likely that you could integrate this explicitly, but it's harder to do so.

Answer 5

By translation, $P(x,y,n) = P(0,y-x,n)$. So, without loss of generality, it is sufficient to consider $P(0,y,n)$.

Let $y = (y_1, \dots, y_d)$ be the coordinate representation of $y \in \Bbb{Z}^d$. We use the signum function, $$ \mathrm{sgn}(x) = \begin{cases} 1,& x > 0 \\ 0,& x = 0 \\ -1,& x < 0 \end{cases} \text{,} $$ generalized to coordinate representations coordinate-wise as $$ \mathrm{sgn}(x_1, \dots, x_d) = (\mathrm{sgn}(x_1), \dots, \mathrm{sgn}(x_d)) $$ and also the absolute value function $$ |(x_1, \dots, x_n)| = (|x_1|, \dots, |x_d|) \text{.} $$

Notice that a shortest path from $0$ to $y$ is

• |y_1| steps of $(\mathrm{sgn}(y_1), 0, \dots, 0)$,
• |y_2| steps of $(0, \mathrm{sgn}(y_2), 0, \dots, 0)$,
• ...
• and, finally, |y_d| steps of $(0, \dots, 0, \mathrm{sgn}(y_d))$.

The total length of that shortest path is $$ n_{\text{shortest}} = |y_1| + |y_2| + \cdots + |y_d| \text{.} $$ Any other path from $0$ to $y$ of length $n_{\text{shortest}}$ is a permutation of that path, of which there are a multinomial coefficient, $$ P(0,y,n_{\text{shortest}}) = \binom{n_{\text{shortest}}}{|y_1|, \dots, |y_d|} = \frac{n_{\text{shortest}}!}{|y_1|! \cdots |y_d|!} \text{.} $$

Any longer path from $0$ to $y$ must contain a permutation of the shortest path as a subpath and the complement of that subpath is some number of cancelling $+1$, $-1$ pairs of steps with both members of a pair acting on the same coordinate. As a consequence, if $n_{\text{shortest}} < n$, if both are even or both are odd, there is a path from $0$ to $y$ of length $n$. However, if one is even and the other odd, there is no path from $0$ to $y$ of length $n$.

Suppose we have a path of length $n > n_{\text{shortest}}$. Then $n$ contains the shortest path, $c_1$ cancelling pairs in the first coordinate, ..., and, finally, $c_d$ cancelling pairs in the $d^\text{th}$ coordinate. In particular, $$ n = n_{\text{shortest}} + 2c_1 + \cdots + 2c_d $$ and the number of such paths is
$$ \binom{n}{|y_1|, \dots, |y_d|,c_1,c_1,\dots,c_d,c_d} = \frac{n!}{|y_1|! \cdots |y_d|! (c_1!)^2 \cdots (c_d!)^2} \text{.} $$ Letting $c_1$, ..., $c_d$ range over all values such that $$ n - n_{\text{shortest}} = 2c_1 + \cdots + 2c_d \text{,} $$ we find the total number of paths of length $n$ is $$ \sum_{\frac{n - n_{\text{shortest}}}{2} = c_1 + \cdots + c_d} \binom{n}{|y_1|, \dots, |y_d|,c_1,c_1,\dots,c_d,c_d} \text{.} $$

We have shown \begin{align*} & P(0,y,n) = \\ &\begin{cases} 0 ,& n < n_{\text{shortest}} \\ \displaystyle \binom{n_{\text{shortest}}}{|y_1|, \dots, |y_d|} ,& n = n_{\text{shortest}} \\ 0 ,& n > n_{\text{shortest}}, n \not\cong n_{\text{shortest}} \pmod 2 \\ \displaystyle \sum_{\frac{n - n_{\text{shortest}}}{2} = c_1 + \cdots + c_d} \binom{n}{|y_1|, \dots, |y_d|,c_1,c_1,\dots,c_d,c_d} ,& n > n_{\text{shortest}}, n \cong n_{\text{shortest}} \pmod 2 \end{cases} \text{.} \end{align*}

We could attempt to analyze the above. However, much easier is to see how $P(0,y,n+2)$ compares to $P(0,y,n)$ once $n > n_{\text{shortest}}$ and for $n \cong n_{\text{shortest}} \pmod{2}$. Each slightly longer path is one of the shorter paths, with a choice of which of the $d$ coordinates gets a cancelling pair, a choice of (up to) $n+1$ locations for inserting the $+1$ in that coordinate, and a choice of (up to) $n+2$ locations for inserting the $-1$. (The locations are "before the first path member", "between the first and second path member", ..., "between the $n-1^\text{th}$ and $n^\text{th}$ path member", and "after the last path member". After inserting the $+1$, the path into which we are inserting the $-1$ is one step longer.) I say "up to" in both cases because inserting a $+1$ in coordinate $i$ anywhere in or on the boundary of a consecutive run of $+1$s in coordinate $i$ produce indistinguishable results. Neverthless, a very loose lower bound on the number of distinct extended paths is $d \cdot 1 \cdot 1$ and a loose upper bound on the number of distinct extended paths is $d \cdot (n+1) \cdot (n+2)$. Consequently, $$ 1 \leq \\ \frac{P(0,y,n)}{P(0,y,n_{\text{shortest}})d^{(n - n_{\text{shortest}})/2}} \leq (n +2 - n_{\text{shortest}})! \text{.} $$ So the rate of growth of $P(0,y,n)$ in $n$ is eventually between exponential, $\sim d^{n/2}$, and factorial, $\sim n!$. (An earlier edit forgot that we were going by $2$s.)

Answer 6

In summary, $(3)$ gives the exact answer, but is harder to compute, and $(5)$ gives a normal approximation to the exact probability distribution.

Convolution

The distribution of the terminal position after $n$ moves is an $n$-fold convolution of the distribution of one move. In $2$ dimensions, this is:

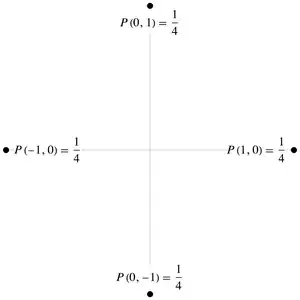
In any dimension, odd $n$ distributes the probability to points whose coordinates have an odd sum (the origin is therefore not included). For example, in $2$ dimensions, for $n=63$:

In any dimension, even $n$ distributes the probability to points whose coordinates have an even sum (the origin is therefore included). For example, in $2$ dimensions, for $n=64$:

In the last two diagrams, the area of the dot is proportional to the number of paths ending at that location.

---

Exact Summation

In the following, $k$ and $p$ are $d$-dimensional multi-indices, $p$ representing the destination position (starting from $0$), and $n=|p+2k|$ is the number of moves to reach the destination (in each of the $d$ dimensions, this means $p+k$ moves toward the destination, and $k$ moves away). Since the components of a multi-index are non-negative, and the number of paths to $(4,-2,6)$ and $(4,2,6)$ are equal, the components of $p$ are the absolute values of the components of the Cartesian position.

Recall that for a $d$-dimensional multi-index $p$, $|p|=\sum\limits_{j=1}^dp_j$ and $p!=\prod\limits_{j=1}^dp_j!$

The number of ways to intersperse the moves along the different axes is $$ \frac{n!}{n_1!n_2!\cdots n_d!}=\frac{|p+2k|!}{(p+2k)!}\tag1 $$ where $n_j=p_j+2k_j$ is the number of moves along axis $j$.

Once we have decided on the way the moves along the different axes are to be interspersed, along axis $j$, there are $\frac{(p_j+2k_j)!}{(p_j+k_j)!\,k_j!}$ ways to arrange the $p_j+k_j$ forward and $k_j$ backward moves. Taking the product across all the axes, we get $$ \prod_{j=1}^d\frac{(p_j+2k_j)!}{(p_j+k_j)!\,k_j!}=\frac{(p+2k)!}{(p+k)!\,k!}\tag2 $$ Thus, when $n\ge|p|$ and $2\mid n-|p|$, we get the total number of paths to be $$ \sum_{|k|=\frac{n-|p|}2}\frac{|p+2k|!}{(p+2k)!}\frac{(p+2k)!}{k!\,(p+k)!}=\bbox[5px,border:2px solid #C0A000]{\sum_{|k|=\frac{n-|p|}2}\frac{n!}{k!\,(p+k)!}}\tag3 $$ out of $(2d)^n$ possible paths.

If $n\lt|p|$ or $2\nmid n-|p|$, then there can be no path to $p$ of length $n$.

Formula $(3)$ is exact, but takes a bit of work to compute. Here are some notes to make the computation more palatable.

Generating Multi-Indices

The difficult part of computing the sum in $(3)$ is generating all the multi-indices. For dimension $d$ multi-indices $p$ so that $|p|=m$, this can be done in the following manner:

Initial multi-index: Start with $p_1=m$ and $p_j=0$ for $1\lt j\le d$.

Subsequent multi-index: Find the lowest order non-zero index, $p_j=a\ne0$. Increment the next index $p_{j+1}=p_{j+1}+1$, set $p_j=0$, and set $p_1=a-1$ (in the case that $j=1$, this simply increments $p_2$ and decrements $p_1$). This process terminates when the lowest order non-zero index is $p_d$ (which would require incrementing $p_{d+1}$).

For example: $d=3$ and $|p|=5$ $$ \begin{array}{|c|c|} p_1&p_2&p_3\\ \hline 5&0&0\\ 4&1&0\\ 3&2&0\\ 2&3&0\\ 1&4&0\\ 0&5&0\\ 4&0&1 \end{array}\qquad \begin{array}{|c|c|} p_1&p_2&p_3\\ \hline 3&1&1\\ 2&2&1\\ 1&3&1\\ 0&4&1\\ 3&0&2\\ 2&1&2\\ 1&2&2 \end{array}\qquad \begin{array}{|c|c|} p_1&p_2&p_3\\ \hline 0&3&2\\ 2&0&3\\ 1&1&3\\ 0&2&3\\ 1&0&4\\ 0&1&4\\ 0&0&5 \end{array} $$ We can use the table generated above and $(3)$ to compute the number of paths to $(0,0,1)$ of length $11$: $$ \begin{align} &\phantom{\,+\,}\frac{11!}{(5!0!0!)(5!0!1!)}+\frac{11!}{(4!1!0!)(4!1!1!)}+\frac{11!}{(3!2!0!)(3!2!1!)}\\ &+\frac{11!}{(2!3!0!)(2!3!1!)}+\frac{11!}{(1!4!0!)(1!4!1!)}+\frac{11!}{(0!5!0!)(0!5!1!)}\\ &+\frac{11!}{(4!0!1!)(4!0!2!)}+\frac{11!}{(3!1!1!)(3!1!2!)}+\frac{11!}{(2!2!1!)(2!2!2!)}\\ &+\frac{11!}{(1!3!1!)(1!3!2!)}+\frac{11!}{(0!4!1!)(0!4!2!)}+\frac{11!}{(3!0!2!)(3!0!3!)}\\ &+\frac{11!}{(2!1!2!)(2!1!3!)}+\frac{11!}{(1!2!2!)(1!2!3!)}+\frac{11!}{(0!3!2!)(0!3!3!)}\\ &+\frac{11!}{(2!0!3!)(2!0!4!)}+\frac{11!}{(1!1!3!)(1!1!4!)}+\frac{11!}{(0!2!3!)(0!2!4!)}\\ &+\frac{11!}{(1!0!4!)(1!0!5!)}+\frac{11!}{(0!1!4!)(0!1!5!)}+\frac{11!}{(0!0!5!)(0!0!6!)}\\[6pt] &=5416026 \end{align} $$ out of $6^{11}=362797056$ paths of length $11$.

---

Normal Approximation

In $\mathbb{Z}^d$, the variance of one move is $\frac1d$. Thus, the variance after $n$ moves would be $\frac nd$. Therefore, the normal approximation would be $$ \left(\frac{d}{2\pi n}\right)^{d/2}e^{-\frac{d}{2n}|x|^2}\tag4 $$ Since the distribution is concentrated only on points where the sum of the components have the same parity as $n$, the distribution should be doubled on those points and zeroed out on the others: $$ \bbox[5px,border:2px solid #C0A000]{\left(1+(-1)^{n-|p|}\right)\left(\frac{d}{2\pi n}\right)^{d/2}e^{-\frac{d}{2n}\|p\|^2}}\tag5 $$ where $\|p\|^2=\sum\limits_{j=1}^dp_j^2$ is Euclidean length.

---

Comparison of the Approaches

$\boldsymbol{n=20}$, $\boldsymbol{d=3}$, and $\boldsymbol{p=(4,2,6)}$:

Formula $(3)$ says the number of paths is $383669852280$ out of the $6^{20}=3656158440062976$ possibilities, giving a probability of $$ \frac{383669852280}{3656158440062976}=\color{#C00}{0.00010493797}\tag6 $$ Formula $(5)$ says that the probability is approximately $$ 2\,\left(\frac3{2\pi\cdot20}\right)^{3/2}e^{-\frac3{2\cdot20}\left(4^2+2^2+6^2\right)}=\color{#C00}{0.00011062678}\tag7 $$ $\boldsymbol{n=50}$, $\boldsymbol{d=2}$, and $\boldsymbol{p=(5,7)}$:

Formula $(3)$ says the number of paths is $3695801675367562256810160000$ out of the $4^{50}=1267650600228229401496703205376$ possibilities, giving a probability of $$ \frac{3695801675367562256810160000}{1267650600228229401496703205376}=\color{#090}{0.0029154735}\tag8 $$ Formula $(5)$ says that the probability is approximately $$ 2\,\left(\frac2{2\pi\cdot50}\right)^{2/2}e^{-\frac2{2\cdot50}\left(5^2+7^2\right)}=\color{#090}{0.0028983731}\tag9 $$ $\boldsymbol{n=100}$, $\boldsymbol{d=5}$, and $\boldsymbol{p=(3,2,3,1,1)}$:

Formula $(3)$ says the probability is $$ \tiny\frac{61550621582025061045069636484697057343625580855166277017112361105163380678323254176105096000000}{10^{100}}\\=\color{#00F}{6.1550622\times10^{-6}}\tag{10} $$ Formula $(5)$ says that the probability is approximately $$ 2\,\left(\frac5{2\pi\cdot100}\right)^{5/2}e^{-\frac5{2\cdot100}\left(3^2+2^2+3^2+1^2+1^2\right)}=\color{#00F}{6.2005276\times10^{-6}}\tag{11} $$

Answer 7

Clearly we can consider just $$ P_{\,d} (0,\left| {{\bf y} - {\bf x}} \right|,n) = Q({\bf z},n,d)\quad \left| \matrix{ \,{\bf y},{\bf x} \in Z^{\,d} \hfill \cr \,{\bf z} \in N^{\,d} \hfill \cr} \right. $$ That is given the $d$-vector $$ {\bf z} = \left( {z_{\,1} ,z_{\,2} , \cdots ,z_{\,d} } \right)^{\,T} \quad \left| {\;0 \le {\rm integer}\,z_{\,k} } \right. $$ you want to count the number of integral lattice paths from the origin to the point $\bf z$, consisting of $n$ steps.

To this regard I suppose that you mean to consider only the paths whose steps are non-negative integers, that is that we are going to count the number of solutions to the diophantine system $$ Q({\bf z},n,d) = {\rm N}{\rm .}\,{\rm of}\,{\rm solutions}\;{\rm to}\;\left\{ \matrix{ 0 \le {\rm integer}\,v_{\,k,\,j} \hfill \cr v_{\,1,\,1} + v_{\,1,\,2} + \cdots + v_{\,1,\,n} = z_{\,1} \hfill \cr v_{\,2,\,1} + v_{\,2,\,2} + \cdots + v_{\,2,\,n} = z_{\,2} \hfill \cr \quad \quad \vdots \hfill \cr v_{\,d,\,1} + v_{\,d,\,2} + \cdots + v_{\,d,\,n} = z_{\,d} \hfill \cr} \right. $$

In fact, if there was no lower bound on the range for $v_{\,k,\,j} $ the nymber of solution to each line would be infinite.
Otherwise, over an infinite support, you shall assign some probability for each step to be effected.

If my interpretation is correct
(unfortunately it would have been too long to put in a comment and ask your preliminary approval)
then the number of solutions to each equation would be the number of weak compositions of $z_k$ into $n$ parts, which is $$ \eqalign{ & \left( \matrix{ z_{\,k} + n - 1 \cr n - 1 \cr} \right) = \left( \matrix{ z_{\,k} + n - 1 \cr z_{\,k} \cr} \right) = \cr & = {{\Gamma \left( {z_{\,k} + n} \right)} \over {\Gamma \left( n \right)\Gamma \left( {z_{\,k} + 1} \right)}} = \cr & = {{\left( {z_{\,k} + n - 1} \right)^{\,\underline {\,n - 1\,} } } \over {\left( {n - 1} \right)!}} = {{\left( {z_{\,k} + 1} \right)^{\,\overline {\,n + 1\,} } } \over {\left( {n - 1} \right)!}} \cr} $$ where $x^{\,\underline {\,k\,} } ,\quad x^{\,\overline {\,k\,} } $ represent respectively the Falling and Rising Factorial

Therefore $$ Q({\bf z},n,d) = \prod\limits_{k = 1}^d {\left( \matrix{ z_{\,k} + n - 1 \cr n - 1 \cr} \right)} = \prod\limits_{k = 1}^d {{{\Gamma \left( {z_{\,k} + n} \right)} \over {\Gamma \left( n \right)\Gamma \left( {z_{\,k} + 1} \right)}}} $$ and the asymptotics will follow easily from the Stirling expression for the Gamma function.

Note that, since we have considered non-negative steps, the expression above is including also paths totally null: thus $Q({\bf z},n,d) $ is actually the number of paths with up to n steps.

Answer 8

Here is an algorithm to compute $P(x,y,n)$ in $O(n^{\lceil d/2\rceil})$ time. It suffices to compute $P(0,a,n)$, which I abbreviate as $P_d(a,n)$. with a subscript to emphasize the dimension. We can show that $$ P_d(a,n)=\sum_{k=0}^n\binom{n}k P_2((a_1,a_2),k)\cdot P_{d-2}((a_3,a_4,\dots,a_n),n-k) $$ The summation variable $k$ represents the number of steps which are in either the $x_1$ or the $x_2$ direction. We choose which of the $n$ steps are in those two directions in $k$ ways, then spend those $k$ steps changing the first two coordinates to $(a_1,a_2)$, and finally use the remaining $n-k$ steps to change the remaining coordinates to $(a_3,\dots,a_n)$.

Now, we can compute $P_2((a_1,a_2),k)$ in $O(1)$ time, since $$ P_2((a_1,a_2),k)=\binom{k}{\frac12(k+a_1+a_2)}\cdot \binom{k}{\frac12(k+a_1-a_2)} $$ with the convention that this is zero when the lower index is fractional. (For a proof, see Number of N step Random walks on 2D infinite grid or lattice). This will require precomputing the first $n$ rows of Pascal's triangle so these binomial coefficients can be looked up in constant time. (For $d\le 2$, the precomputation is not necessary).

All that remains is to compute $P_{d-2}((a_3,a_4,\dots,a_n),n-k)$ for each $k$. There are $O(n)$ terms to compute, and by induction each can be computed in $O(n^{\lceil d/2\rceil-1})$ time, so the entire sum is doable in $O(n^{\lceil d/2\rceil})$ time.