2

There is this following statement which I need to evaluate to be true or false:

Let $f(x) $, $f:\mathbb{R} \rightarrow \mathbb{R_+} $ be a continuous probability density function. Then $\lim_{x\to\infty} f(x) = 0 $.

I understand this is true, because since $ \lim_{x\to\infty} F_X(x) = 1 $ it's necessary that: $$\lim_{x\to\infty} f(x) = \lim_{x\to\infty} \frac{dF_X}{dx} = 0 $$

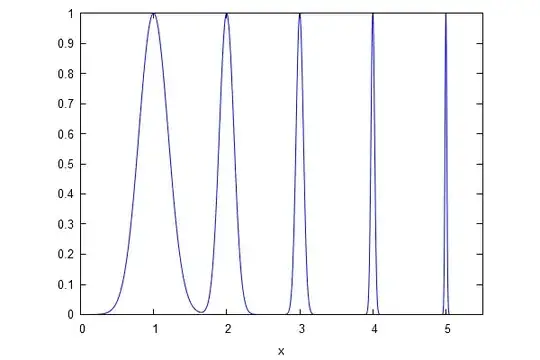
A friend of mine has proposed an counterxample: you have a triangle with area $1/2$ and height $1$ and, after every unity in $x$ axis, you have another triangle, with area $1/2^n$. Since the height is fixed in $1$, we can say it is a probability density function. It is also continuous, except for a countable set of numbers in which it is not continuous (that is, when $\lim_{x\to a^-} f(x) = 0 $ and $\lim_{x\to a^+} f(x) = 1 $). He says in this case $f$ doens't necessarily tend to $0$ as $x\to \infty$.

Still, in my point of view, I can say that $\lim_{x\to\infty} f(x) = 0 $ except for a countable set of elements. To me, it's just an example that $\lim_{x\to\infty} f(x) = 0 $, except for a countable set of elements. Does it make sense? Who is right?

Thank you!

leonbloy
  • 63,430
YetAnotherUsr
  • 526

2 Answers2

3

Your proof is wrong, because, in general, $\lim_{x \to \infty}h(x) = 1$ does not imply $\lim_{x \to \infty}h'(x) = 0$ . See here.

And indeed, the statement is false. The intuition of your friend is on the right track. Here's a continuous (and smooth) example:

We have a set of random variables $(X_1,X_2, X_3 \cdots)$, where each $X_k$ follows a normal density with mean $\mu=k$ and stardard deviation $2^{-k}/\sqrt{2 \pi}$, so that

$$f_{X_k}(x) =2^k \exp \left({- (x-k )^2 2^{2k}\pi } \right) $$

Let $f_X(x)$ be a mixing of such normal rvs, weighted by exponentially decreasing factors:

$$f_X(x) = \sum_{k=1}^{\infty} \frac{1}{2^{k}} f_{X_k}(x)= \sum_{k=1}^{\infty} \exp \left({- (x-k )^2 2^{2k}\pi } \right)$$

This is a valid continuous density: it corresponds to picking randomly one of $(X_1,X_2, X_3 \cdots)$, with the probability of picking $X_k$ being $1/2^{k}$.

But $f_X(n) > 1$ for any positive integer $n$. Hence its limit cannot be zero.

enter image description here

leonbloy
  • 63,430
  • This is OK, but needlessly complicated. The "triangle" example works fine. – David Apr 30 '19 at 01:54
  • @David It's basically the same thing. I find the triangles more complicated, but I guess that's a matter of taste. – leonbloy Apr 30 '19 at 02:02
  • Thanks, it's nice to have other counterexamples! Your link helped a lot as well. – YetAnotherUsr Apr 30 '19 at 02:50
  • @leonbloy I was thinking, would it work for the series $ \sum_{n=1}^{\infty} (2^{-n}) f_{X_n}(x) $ as well? And in a more general case: if I have any other density with growing mean indexed in $n$ and decreasing variance, will it work as a counterexample? Thanks! – YetAnotherUsr May 01 '19 at 01:16
  • I will try once I get home with other distributions, but it made me curious to think which would be the "minimal" criteria a probability function should meet in order to work as a counterexample to this. – YetAnotherUsr May 01 '19 at 01:18
  • @M.Gonzalez Other densities could work, of course. The important thing is not the mean and variance (it would work with a Cauchy distribution, which has infinite variance and no mean) but the mode. We just want the mode ocurring at increasing positions, and its value increasing as $2^k$. – leonbloy May 01 '19 at 01:22
  • I will try later with a Cauchy distribution! But mind I ask: how precisely you know the mode occurring at increasing positions and increasing as $2^k$ (or any other way I am weighting) is the condition for this working? – YetAnotherUsr May 01 '19 at 01:32
  • Well', if you followed my proof that should be evident. In my example, the modes are at $x=k$ and have values $\alpha 2^k$ (in my case $\alpha=1$, but that didn't matter), which cancel with the weights. In that way, we have build an increasing unbounded sequence $x_k$ (the modes) for which $f(x_k) \ge \alpha$, and so $f(x)$ cannot tend to zero. – leonbloy May 01 '19 at 02:16
  • Thank you @leonbloy! – YetAnotherUsr May 02 '19 at 21:11
1

I'm not sure that "the limit is zero except for a countable set of points" makes any sense. It just says that the limit is not zero, and your friend is right.

Furthermore, it's not in fact true that "the limit is zero except for a countable set of points". To make this clear, let's write your friend's construction a bit more precisely. The graph of $f$ consists of

  • a triangle with base the interval $[0,1]$ and height $1$ occurring at $x=0$;
  • a triangle with base $[1,1\frac12]$ and height $1$ occurring at $x=1$;
  • a triangle with base $[2,2\frac14]$ and height $1$ occurring at $x=2$;
  • a triangle with base $[3,3\frac18]$ and height $1$ occurring at $x=3$;
  • and so on, with $f(x)=0$ for all $x$ outside these triangles.

Then the total area under the graph is $1$ as stated. Moreover, $f(x)$ is at least $\frac12$, and therefore does not tend to zero, for all $x$ in $$[0,\tfrac12]\cup [1,1\tfrac14]\cup [2,2\tfrac18]\cup\cdots\ ,$$ and this is not countable.

Note also that if the lack of continuity bothers you, you can construct an example where the peaks of the triangles are at $\frac12,\,1\!\frac14,\,2\frac18,\,3\frac1{16}$ and so on, and this will have similar properties.

David
  • 82,662