I'm stuck trying to solve this problem:
"Given positive integers $m, n, m', n'$ such as $m/n < m'/n'$ and $m'n - mn' = 1$, we define $$a/b = (m+m')/(n+n').$$ Check that $m/n < a/b < m'/n'$ and prove that $$gcd(a, b) = 1."$$
The way I see it, it must be that $a = m+m'$ and $b = n+n'$. But I'm not sure how to prove the $gcd(a,b) = 1$ part. Any help would be appreciated.
Hint: $\ (m+m')\,n - m\,(n'+n) = m'n-mn'= 1$,
It is clear when viewed as a column operation preserving a determinant
$$\left|\begin{array}{} m'+m & m\\ n'\,+\,n & n\end{array}\right|\,=\,\left|\begin{array}{} m' & m\\ n' & n\end{array}\right|\qquad $$
Note $ $ This Farey mediant operation has a natural geometric interpretation as a change of basis:
$\quad \dfrac{m}n,\,\dfrac{m'}{n'}\,$ are Farey adjacent $\!\iff\! \begin{align}u &= (n,\ m)\\ v &= (n',m')\end{align}$ are a basis of $\,\Bbb Z^2$ $\!\iff\! |\det(u,v)| = 1$
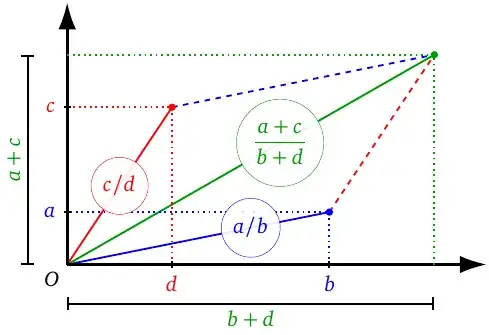
This has a pretty proof via Pick's Area theorem, e.g. see here and here. The mediant operation yields the diagonal $\,u\!+\!v\,$ of the fundamental parrallelogram with sides $\,u,v\,$ and we obtain another basis by replacing one side by the diagonal, i.e. $\, u,v \to u\!+\!v,\,v$, depicted below (from Wikipedia)
$\qquad\qquad $ 
