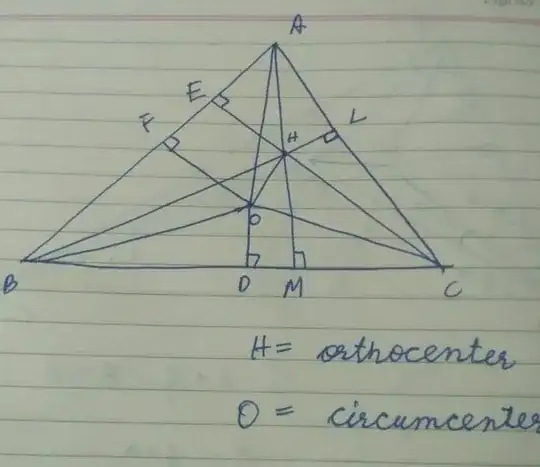
What is wrong with the solution of 'Find that the distance between the circumcenter and the orthocenter of triangle ABC'.
This is NOT a duplicate of - Distance between orthocenter and circumcenter.
As O is circumcenter $ \angle BOD = \angle A$
$\angle OBD = 90$° - A
$\angle ABL = 90°- A$ ( $ \angle ALB is 90 degrees)
$B = -2A + \pi + \angle OBL$
$\angle OBL = B + 2A - \pi$ now using sine rule in triangle OHB
$OH = - sin(\pi - (2A+B) 2R$
$OH = - 2Rsin(2A+B)$
But the answer is R $ \sqrt{1-8\ cosA \ cosB \ cosC} $
maybe my answer is correct but just in the correct form.