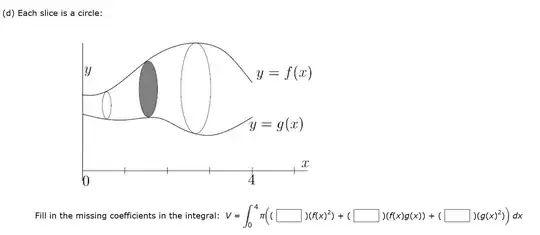
I am encountering a very tricky problem for me and I am not sure the right approach to solve it. It is simple. It is just telling me to fill in the coefficients of the integral to find the volume of the figure. But I honestly do not how to approach it. I would really really appreciate any help! Thank you!
the link to a screenshot is below: