Is it possible to find the maximum clique more efficiently in a matrix with 4 identical triangles?
As an example consider a matrix below where:
$$A_{12} = A_{21}\,,~ A_{1n} = A_{n1}\, ,~ \ldots$$
and
$$A_{11} = A_{nn}\,,~A_{12} = A_{n-1\,n}\,,~ \ldots$$
The maximum clique problem is NP complete and all known algorithms take exponential time; this isn't going to change for your class of matrices, because it is very general.
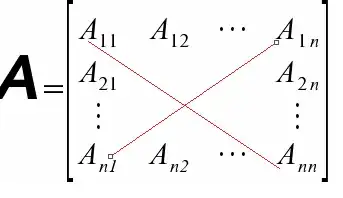
In particular, for any graph $G$ with adjacency matrix $A_G$, the matrix $$\begin{bmatrix}A_G & 0 \\ 0 & A_G' \end{bmatrix}$$ (where $A_G'$ denotes the matrix $A_G$ with all rows and columns reversed) satisfies your condition. It represents a graph consisting of two disjoint copies of $G$.
In this graph, the maximum clique is the same as the maximum clique in one copy of $G$, and so we're solving the maximum clique problem for an arbitrary graph of size $\frac n2$. As a result, if the best maximum clique algorithm takes time $\Theta(C^n)$, the best algorithm for your class of graphs can't do better than time $\Theta(C^{n/2})$.
We can think of your condition as saying that the map $\phi :V(G) \to V(G)$ which reverses the order of the vertices (if $V(G) = \{v_1, \dots, v_n\}$ then $\phi(v_i) = v_{n+1-i}$) is an automorphism of $G$. So we might be able to speed up the search for a clique slightly, in a way that depends on your algorithm but probably isn't too significant. For example, if we're using a brute-force search, we can cut the search space in half by not checking the set $\phi(S)$ for being a clique if we've already checked the set $S$.
