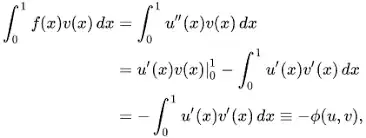Part 1: General Explanation
Your question is a pretty common one.
First the important part of finding weak solutions to PDEs is rewriting a PDE into the weak form aka
\begin{align}
L(x)=0 \Rightarrow \int L(x)v \ dx=0
\end{align}
where $L$ is some differential operator (using the integration by parts bit makes finding numerical solutions easier but it is not strictly nessary). From the fundamental lemma of calculus of variations for the integral to be equal to zero for any continuously compactly supported function $v$, $L(x)$ must be equal to zero. By writing the PDE in this form any true solution is also a solution to the weak form, but not every weak form solution is a true solution to the original PDE problem. If you want a nice example of what I am talking about see the answer to this post. In general though the weak solution can be very different from the true solution (they do come from different function spaces very all). One of the major realizations in the practical applications of PDEs to real world problems was that the weak solution of a PDE is often "Good Enough". I had a book that talked about the history of this but I can't find it :( .
For many problems solutions that come from the Sobolev space (from which weak solutions come from) is "Good Enough". As nicely summarized in this post
For instance, in the case of the heat equation, often it is desired to
know how much heat energy is in the tank at a given time, what the
flux of heat energy out of the domain is, how rapidly it will lose the
energy it had to begin with, etc. In physical applications, rarely is
the specific point value of a function important - it is averages over
small patches in both time and space, which are integrals.
In general the true solution is much more specific while the weak solution cares more about preserving areas and volumes rather than function values.
One thing that is not mentioned in your post but is really important is that once it the appropriate form you can discretize your weak solution using the Galerkin method (this is a really important part of the finite element). Applying the Galerkin method it reduces the problem of finding the weak solution to just finding the value of your unknown function on the nodes of your mesh (which is a linear algebra problem). If you are taking a course in FEM most of the time spent in the course is devoted to this. There are different ways discretizing a PDE or PDE that is independent of FEM (most of these fall under the umbrella of Finite difference methods). In general FEM is best if you have a simple PDE (or well studied PDE like the Naiver Stokes Equation) but have a very complex boundary (e.g. a 3D model of a bone, a map of a continent). This discretion step coupled with a weak formulation allows you to find a solution to most PDEs on any finite boundary.
Part 2: Answering Questions
In this section I am just going to answer some of the questions you raised.
But this can't be the only reason why weak forms are used.
Mainly it is (for engineers). For mathematicians putting a PDE into the weak form helps identify which function space a solution belongs to (odern PDE research is often devoted to understanding what functions make up the solutions to a PDE rather than finding the solution to a PDE). Applying the finite method refines it further, allowing you to look through a "smaller" functional space.
Solution to the weak form has to approximate the solution to the original problem as well.
As explained previously it does as far as areas, volumes and potential energy is preserved. There are many ways to approximate a PDE(e.g. finite difference methods, spectral methods) weak solutions aren't the only way. For some PDEs the weak solution is a poor approximation of the true solution (this is beyond the scope of your question, unless you do graduate work in certain areas you will probably never see PDEs like this, just know that there are some really strange functions, ODEs, and PDEs).
Why does it make sense that a solution to the weak form of the problem is anywhere related to the solution of the original problem?
There are two different ways of looking at this question
- Read a numerics theorem that says the finite element method will converge to a solution such that the residual (then norm of $L(x)$) will be minimized.
- Think about a problem like this
Equations of the theory of elasticity need to be solved in a given domain for finding an equilibrium configuration of a deformable elastic body. This is a strong form of the problem. At the same time, the total mechanical energy (strain energy of the body + potential energy of externally applied forces) is at minimum in an equilibrium state, which means that a certain functional needs to be minimized with respect to the unknown field of displacements for finding the solution. This is a weak form (one among many possible). Both formulations are mathematically equivalent, but allow for different numerical methods for finding approximate solutions. Typically, one uses finite difference method for solving differential equations and FEM for minimizing the total energy.
- Then apply the Lax-Milgram Theorem to the weak form. The theorem works because function spaces are vector spaces and we can apply the results of linear algebra to the weak form (if it is linear or bilinear).
If we multiply to sides of the equation by some function, integrate, and find a solution that satisfies this new relation, why does it seem to imply it approximately solves the original problem as well?
This is one way of thinking about the weak solution of a PDE.
I also remembered from a math lecture some years ago that the integral of a function multiplied by the Dirac delta over some point (and Dirac delta has an integral of one!) equals the value of the function at the point the Dirac is located. Does this have anything to do with the reason why the solution to the weak formulation works?
This is related to the theory of distributions and how they can be thought of as generalizations of functions. It is a bit of a side note in the theory of PDEs and functional analysis, I would put this idea in a box for now and think about it in the future when you cover distributions (which you could study in their own course). The fundamental lemma of calculus of variations is more important for understanding how weak solutions work.
Additional Notes
- It might be helpful if you read some of the answers to my recent FEM
question
- If you desire to know the theory in detail I recommend reading PDEs by L. Evans. It has the answer to almost any theoretical PDE question. My goal when answering you questions was to make things accessible, if you want full details Evans does a better job than anyone else.