2

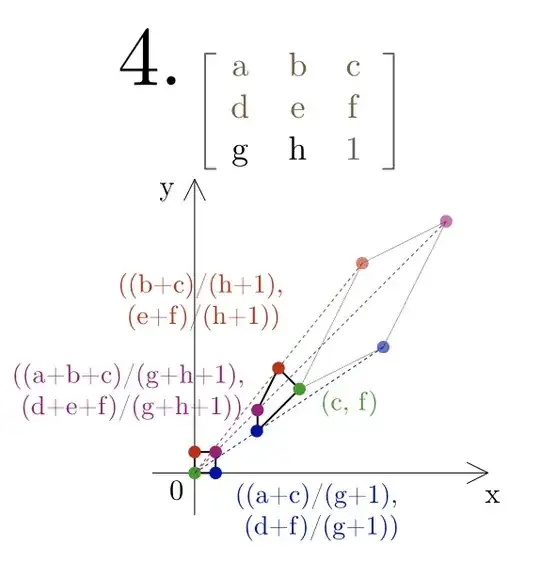
In this answer from Pedro Gimeno he proposed the following transformation to map the points of any arbitrary quadrilateral to the unit square

$$\pmatrix{x'\\y'} = > \pmatrix{u_x&v_x&w_x\\u_y&v_y&w_y}\pmatrix{x\\y\\xy}$$

$$x'=u_xx+v_xy+w_xxy\\ y'=u_yx+v_yy+w_yxy$$

It transforms the unit square in a way controlled by the vectors $u=(u_x,u_y), v=(v_x,v_y), w=(w_x,w_y)$ as follows:

Geometric interpretation of u, v, w (sorry, I can't post images)

However, I'd like to do the opposite. I need to integrate on an arbitrary quadrilateral and I'd like to define my integral on the unit square and then map the coordinates of the unit square on the original quadrilateral .

The matrix Pedro proposed, however, is not invertible and I'm not sure a pseudo-inverse matrix is what I'm looking for.

How can I obtain the opposite transformation?

Xander Henderson
  • 29,772
Luca
  • 183
  • Start with the rectangle. Translate any vertex to the origin. Rotate to make one of the two edges at the origin lie on the $x$-axis. Scale both axes to make the rectangle the unit square. These are all invertible operations. – Ethan Bolker Apr 17 '19 at 13:42
  • I'm utterly sorry. i don't know why, while writing the question, I wrote rectangle instead of quadrilateral. The question is about arbitrary quadrilateral. For rectangles would be trivial. – Luca Apr 17 '19 at 13:45
  • You my find another route to a solution of your integration problem starting from a search for barycentric coordinates quadrilateral. For example: https://numfactory.upc.edu/web/FiniteElements/Pract/P4-QuadInterpolation/html/QuadInterpolation.html – Ethan Bolker Apr 17 '19 at 13:52
  • 1
    If you want the map to be invertible, a planar projective transformation is easy to compute. See https://math.stackexchange.com/a/339033/265466. – amd Apr 17 '19 at 19:10
  • Since @EthanBolker proposed different strategies for integration, I decided that it would have been probably the best thing to do to move the question "to a higher level" and to be a bit less specific. I therefore opened this question: https://math.stackexchange.com/q/3192164/162091 Please, feel free to close or delete this one – Luca Apr 18 '19 at 09:08

3 Answers3

2

Perhaps, you could use perspective projection matrix in homogenous coordinates.

Perspective transformation matrix, transforming uniq square

Reversing this operation is just a matter of finding an inverse of this transformation matrix.

This will work for many cases. However, it doesn't map to any quadrilateral. For one, I think, the quadrilateral will still have to be convex.

(Image source: Wikimedia Commons, Author: D.stebani, License: CC BY-SA 4.0)

Andriy Makukha
  • 171
1

One possible strategy.

Parameterize each side of your (convex) quadrilateral $ABCD$ using

$A + t(B-A)$,

$D + t(C-D)$,

$A + s(D-A)$,

$B + s(C-B)$

with $P = (s,t)$ in the unit square. To map $P$ to the quadrilateral, join the points determined by $t$ on $AB$ and $DC$, the points determined by $s$ on the other two edges, and find the intersection of those two line segments.

Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
  • This is a very good starting point for what I had in mind. Probably with a bit of algebra I can obtain a system of equation to find (x,y) given (s,t). I’ll elaborate starting from this. – Luca Apr 17 '19 at 15:09
  • Isn’t this exactly the transformation cited in the question, albeit with an image in $\mathbb R^3$? – amd Apr 18 '19 at 18:06
  • @amd It might well be. I didn't read that one since the OP rejected it. This geometric (re)statement at and comments in the new question https://math.stackexchange.com/questions/3192164/how-to-integrate-over-arbitrary-quadrilateral may actually be of use. – Ethan Bolker Apr 18 '19 at 20:32
0

That answer transforms the unit square into an arbitrary quadrilateral. If you only want a rectangle, you can just use: $$\begin{pmatrix}x' \\ y' \end{pmatrix} = \begin{pmatrix} u_x & v_x \\ u_y & v_y \end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix}$$ which is invertible assuming $u$ and $v$ are linearly independent. This assumes one of the corners of your rectangle is at the origin, otherwise you will also need to do a translation.

kccu
  • 20,808
  • 1
  • 22
  • 41
  • I'm utterly sorry. i don't know why, while writing the question, I wrote rectangle instead of quadrilateral. The question is about arbitrary quadrilateral. For rectangles would be trivial as you correctly pointed out – Luca Apr 17 '19 at 13:45