I am having trouble solving this integral with complex analysis
$$\int\limits^{\infty }_{0}\frac{e^{iax}}{x^{2} +1} dx$$
I have tried two different contours; those being
with both contours, I got the answer $\int\limits ^{\infty }_{0}\frac{e^{iax}}{x^{2} +1} dx=\frac{\pi }{2e^{a}}$ But according to wolfram alpha's approximation, this is wrong. Wolfram alpha had a real and imaginary part to the answer. So I'm confused. Can someone show the process for solving this with contour integration?
$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} &\mbox{Note that} \\[2mm] &\ \left.\int_{0}^{\infty}{\expo{\ic ax} \over x^{2} + 1}\,\dd x \,\right\vert_{\ a\ \in\ \mathbb{R}} \\[2mm] = &\ \underbrace{\int_{0}^{\infty}{\cos\pars{\verts{a}x} \over x^{2} + 1}\,\dd x}_{\ds{\pi\expo{-\verts{a}} \over 2}}\ +\ \ic\,\mrm{sgn}\pars{a} \bbox[10px,#ffd]{\Im\int_{0}^{\infty}{\expo{\ic\verts{a}x} \over x^{2} + 1}\,\dd x}\label{1}\tag{1} \end{align}
$\ds{\mrm{E}_{1}}$ is the Exponential Integral.
Then, \begin{align} &\bbox[10px,#ffd]{\Im\int_{0}^{\infty}{\expo{\ic\verts{a}x} \over x^{2} + 1}\,\dd x} \\[5mm] = &\ -\,{1 \over 2}\,\expo{-\verts{a}}\bracks{% \mrm{P.V.}\int_{-\verts{a}}^{\verts{a}}{\expo{-y} \over y}\,\dd y + \mrm{E}_{1}\pars{\verts{a}}} + {1 \over 2}\,\expo{\verts{a}}\ \mrm{E}_{1}\pars{\verts{a}} \\[5mm] = &\ -\,{1 \over 2}\,\expo{-\verts{a}} \int_{0}^{\verts{a}}\pars{{\expo{-y} \over y} + {\expo{y} \over -y}} \,\dd y + \sinh\pars{\verts{a}}\mrm{E}_{1}\pars{\verts{a}} \\[5mm] = &\ \expo{-\verts{a}} \int_{0}^{\verts{a}}{\sinh\pars{y} \over y}\,\dd y + \sinh\pars{\verts{a}}\,\mrm{E}_{1}\pars{\verts{a}} \\[5mm] = &\ \expo{-\verts{a}}\,\mrm{Shi}\pars{\verts{a}} + \sinh\pars{\verts{a}}\,\mrm{E}_{1}\pars{\verts{a}} \label{2}\tag{2} \end{align}
$\ds{\mrm{Shi}}$ is the Hyperbolic Sine Integral.
The exponential integral $E_1(z):=\int_z^\infty\frac{e^{-t} dt}{t}=e^{-z}U(1,\,1,\,z)$ in terms of a confluent hypergeometric function of the second kind. Since $\frac{1}{x^2+1}=\frac{i}{2}\sum_\pm\frac{\pm 1}{x\pm i}$, your integral is $$\frac{i}{2}\sum_\pm\pm\int_0^\infty\frac{e^{iax}dx}{x\pm i}=\frac{i}{2}\sum_\pm\pm e^{\pm a}\int_{\pm a}^\infty\frac{e^{-z}dz}{z}\\=\frac{i}{2}\sum_\pm\pm e^{\pm a}E_1(\pm a)=\frac{i}{2}\left(U(1,\,1,\,a)-U(1,\,1,\,-a)\right).$$This isn't real, but its real part is $-\frac{\pi}{2}e^{-a}$ for $a>0$. This means I probably have a sign error somewhere editors are welcome to address, since $$\int_0^\infty\frac{\cos axdx}{x^2+1}=\frac12\Re\int_{\Bbb R}\frac{e^{iax}dx}{x^2+1}=\frac{\pi}{2}e^{-|a|}$$is a useful sanity check based on the Cauchy distribution's characteristic function.
I can't directly use contour integration to solve this, but I can use Fourier Transforms and their properties.
$$\begin{align*}I(a) &= \int_0^\infty \dfrac{e^{iax}}{x^2+1} dx \\ \\ &= 2\pi \int_0^\infty \dfrac{e^{i2\pi sa}}{\left(2\pi s\right)^2 +1} ds \\ \\ &= \pi \int_{-\infty}^\infty H(s)\dfrac{2}{\left(2\pi s\right)^2 +1} e^{i2\pi sa}ds \\ \\ &= \pi \mathscr{F}^{-1}\left\{H(s)\dfrac{2}{\left(2\pi s\right)^2 +1}\right\}\\ \\ &= \pi \cdot \mathscr{F}^{-1}\left\{H(s)\right\}*\mathscr{F}^{-1}\left\{\dfrac{2}{\left(2\pi s\right)^2 +1}\right\}\\ \\ &= \pi \cdot \dfrac{1}{2}\left[\dfrac{1}{i\pi(-a)} + \delta(-a)\right] * e^{-|a|}\\ \\ &= \dfrac{\pi}{2} e^{-|a|} + \dfrac{i}{2} \dfrac{1}{a} * e^{-|a|}\\ \\ &= \dfrac{\pi}{2} e^{-|a|} + \dfrac{i}{2} \int_{-\infty}^\infty \dfrac{e^{-|\tau|}}{a-\tau} d\tau\\ \\ &= \dfrac{\pi}{2} e^{-|a|} + \dfrac{i}{2} \int_0^\infty \dfrac{e^{-\tau}}{a-\tau} d\tau+ \dfrac{i}{2} \int_{-\infty}^0 \dfrac{e^{\tau}}{a-\tau} d\tau\\ \\ &= \dfrac{\pi}{2} e^{-|a|} - \dfrac{i}{2} \int_{-a}^\infty \dfrac{e^{-(t+a)}}{t} dt - \dfrac{i}{2} \int_{\infty}^a \dfrac{e^{(a-t)}}{t} dt\\ \\ &= \dfrac{\pi}{2} e^{-|a|} - \dfrac{i}{2}e^{-a} \int_{-a}^\infty \dfrac{e^{-t}}{t} dt + \dfrac{i}{2} e^{a}\int_a^{\infty} \dfrac{e^{-t}}{t} dt\\ \\ &= \dfrac{\pi}{2} e^{-|a|} + \dfrac{i}{2}e^{-a} \mathrm{Ei}(a) - \dfrac{i}{2} e^{a}\mathrm{Ei}(-a)\\ \\ &= \dfrac{\pi}{2} e^{-|a|} -i \space \dfrac{e^{a} \mathrm{Ei}(-a) - e^{-a}\mathrm{Ei}(a)}{2}\\ \end{align*}$$
This answer looks like what @J.G. was driving at.
Note that just deriving the inverse Fourier Transform of the Heaviside unit step, $H(s)$, involves multiple contour integrations and distribution theory.
In contour 1, I am guessing you treated the integral along the segment $C1$ as zero, but it is not, and it has a non-zero imaginary part.
Similarly, the same integral, with imaginary result, is omitted along $C1$ in contour 2.
The integral does not have a real value.
Here is a solution of the integral
$$I(a>0) = \int_{0}^{\infty} f(x)\;dx\tag{1a}$$ where $$f(x) = \frac{e^{i a x}}{1+x^2}\tag{1b}$$
using contour integration. It is almost identical to the attempt of the OP but I use a slightly modified version of the contour 2 of the OP and it looks like that:
The path of integration is the closed contour $\Gamma =\gamma_1 + \gamma_2 + \gamma_3 + \gamma_4 + \gamma_5$
As there are no singularities of $f(z)$ included in or on the contour $\Gamma$ the integral over the contour is zero by means of Cauchy's theorem.
In the following, and integral corresponding to the path $\gamma_k$ is called $I_k$.
Cauchy's theorem then means just that $\sum_{k=1}^{5} I_k = 0$.
What follows is a comprehensive description of the paths in question:
$\gamma_1$ = positive real axis from $x=0$ to $x=R >1$ (in the limit $R \to \infty$ this becomes the integral I(a))
$\gamma_2$ = quarter circle of radius $R(>1)$ in mathematical positive direction from $R$ to $i R$. With the parametrization $z=R e^{i \phi}$, $dz = R e^{i \phi} d\phi$, $\phi = 0 \cdots \pi/2$ we get
$$I_2 = \int_{0}^{\pi/2} R e^{i \phi} \frac{e^{i a R e^{i \phi}}}{1+R^2 e^{i \phi}} \;d\phi\tag{2a}$$
We can estimate the modulus of $I_2$ as follows
$$\begin {align}|I_2|& \le \int_{0}^{\pi/2} R |e^{i \phi}| \frac{|e^{i a R e^{i \phi}}|}{|1+R^2 e^{i \phi}|} \;d\phi = \int_{0}^{\pi/2} R \frac{|e^{i a R cos(\phi) + i a R (i sin(\phi) }|}{|1+R^2 e^{i \phi}|} \;d\phi\\&=\int_{0}^{\pi/2} R \frac{e^{- a R sin(\phi) }}{|1+R^2 e^{i \phi}|} \;d\phi \le \int_{0}^{\pi/2} R \frac{1}{|1+R^2 e^{i \phi}|} \;d\phi\\ &\le \int_{0}^{\pi/2} \frac{R}{R^2-1} \;d\phi=\frac{\pi}{2} \frac{R}{R^2-1}\end{align} \tag{2b}$$
In the last step we have used the inverse triangle inequality $|A+B| \ge ||A| - |B||$.
Hence we have obtained that $|I_2|\le \frac{\pi}{2}\frac{R}{R^2-1} $, and we conclude that $I_2$ vanishes in the limit $R\to \infty$.
$\gamma_3$ = imaginary axis from $z=i R$ to $z=i(1 + \epsilon)$, $0 \lt \epsilon <<1$. The parametrization $z = i y$, $dz=i dy$, $y=R \cdots (1+\epsilon)$ leads in the limit $R \to \infty$ to
$$I_3 = - i \int_{1+\epsilon}^{\infty} \frac{e^{- a y}}{1-y^2}\;dy\tag{3}$$
$\gamma_4$ = small half circle of radius $\epsilon$ avoiding the pole at $z=i$ The parametrization $z = i + \epsilon e^{i \phi}$,$dz =i \epsilon e^{i \phi}d\phi $, $\phi = \pi/2 \cdots (-\pi/2)$) leads to
$$I_4 = - i \epsilon \int_{-\pi/2}^{\pi/2}e^{i \phi} \frac{e^{i a (i+ \epsilon)e^{i \phi}}}{1+(i + \epsilon\; e^{i \phi})^2} \;d\phi\tag{4a} $$
For $\epsilon \to 0$ this becomes
$$I_4 = -\frac{1}{2} \int_{-\pi/2}^{\pi/2} e^{i a (i)}\;d\phi =- \frac{\pi}{2} e^{-a}\tag{4b}$$
$\gamma_5$ = imaginary axis from $z=i(1-\epsilon)$ to $z=0$.
The parametrization $z = i y$, $dz = i dy$, $y = 1-\epsilon \cdots 0$ leads, similar to $I_3$, to
$$I_5 = - i \int_{0}^{1-\epsilon}\frac{e^{- a y}}{1-y^2}\;dy\tag{5}$$
With the reults obtained so far and Cauchy's theorem this leads to the following expression for the integral $I(a)$
$$I(a) = - I_4 - (I_3+I_5) = \frac{\pi}{2} e^{-a}+ i \lim_{\epsilon \to 0} (\int_{0}^{1-\epsilon} \frac{e^{- a y}}{1-y^2}\;dy+\int_{1+\epsilon}^{\infty} \frac{e^{- a y}}{1-y^2}\;dy)\tag{6}$$
Extracting real and imaginary part we have
$$\Re(I(a)) = \frac{\pi}{2} e^{-a}\tag{7a}$$ $$\Im(I(a)) = \lim_{\epsilon \to 0} (\int_{0}^{1-\epsilon} \frac{e^{- a y}}{1-y^2}\;dy+\int_{1+\epsilon}^{\infty} \frac{e^{- a y}}{1-y^2}\;dy) = P.V. \int_{0}^{\infty} \frac{e^{- a y}}{1-y^2}\;dy\tag{7b}$$
In the last step we have used the definition of Cauchy's principal value of the integral with respect to the point $y=1$.
Hence we have derived an expression for the imaginary part of our integral which was missing in the OP.
But now it needs to be calculated.
Mathematica gives for the imaginary part this closed expression
1/2 Sqrt[\[Pi]] MeijerG[{{1/2}, {}}, {{1/2, 1/2}, {0}}, a^2/4]
An equivalent expression using better known special functions is
$$\Im(I(a)) = \frac{1}{2}\left(e^{-a} \text{Ei}(a)-e^{a} \text{Ei}(-a)\right)\tag{8}$$
It can be derived using the definition
$$\text{Ei}(t)=\int\frac{e^{t}}{t}\,dt\tag{9}$$
of the exponential integral.
Finally, here is a plot of the integral $I(a)$
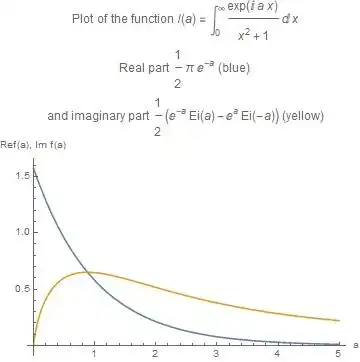
Discussion
§1. Here we investigate the OP's choice of contour 2.
In contour 2 the path $\gamma_2$ is a straight line between $z=R$ and $z=i R$, instead of the quarter circle. If parametrized as $z= R(t+i (1-t))$, $0<t<1$ this leads to the integral
$$I_{2,OP} = \int_0^1 \frac{(1-i) R e^{i a R (t+i (1-t))}}{1+R^2 (t+i (1-t))^2} \, dt$$
which (for $a>=0$) goes to zero for $R\to\infty$ as can be shown by estimating the modulus of the integral as before.
§2. Just noting a compact description of integration path (c.f. @DonAntonio) $$\begin{align}&\Gamma_{\epsilon,R}=\gamma_1:=[0,R]\cup\gamma_2:=\{Re^{i \phi},\phi \in [0,\pi/2]\}\cup\gamma_3:=[i R,i(1+\epsilon]\\&\cup\gamma_4:=\{\epsilon e^{i\phi},\phi \in [\pi/4, -\pi/4]\}\cup\gamma_5:=[i \epsilon,i 0],(\epsilon,R)\in\Bbb R^+\end{align}$$
