2

A container contains $5$ red balls. On each turn,one of the balls is selected at random,painted blue,and returned to the container.The expected number of turns it will take before all $5$ balls are colored blue is $\frac{m}{n}$,where $m$ and $n$ are relatively prime positive integers.Find $m+n$

It appears that the problem is made keeping some theory of expectation but I can't figure out what it really is

Maverick
  • 9,172
  • 2
  • 30
  • 61

2 Answers2

4

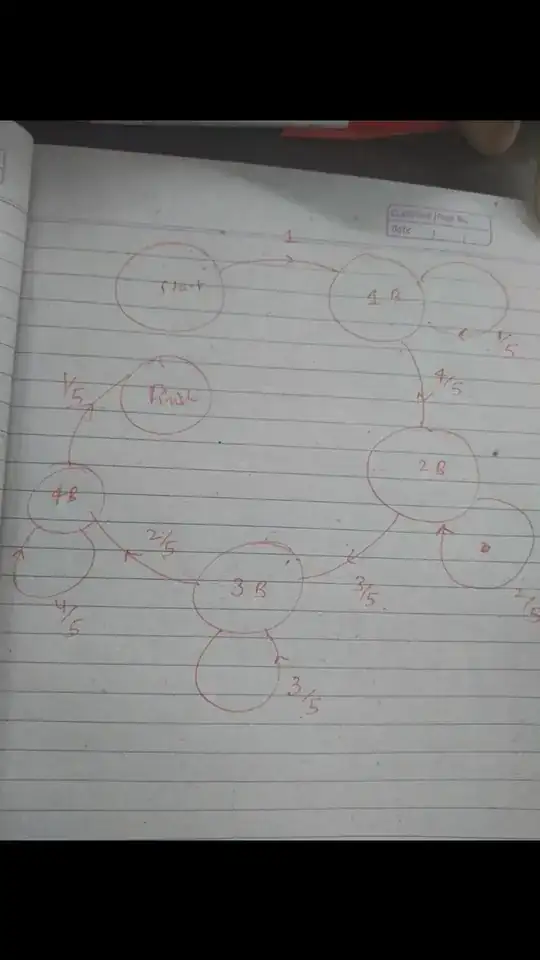
Let $E(n)$ be the expected number of turns to turn the balls blue, assuming there are $n$ red balls left and $5-n$ blue balls. Thus, the problem is to find $E(5)$. Clearly, $E(5) = E(4) + 1$, as a red ball will definitely be turned into a blue ball. Then, $E(4) = 1+\frac{4}{5}E(3)+\frac{1}{5}E(4)$, as there is a $\frac{4}{5}$ probability of picking a red ball and turning it blue, and a $\frac{1}{5}$ probability of picking a blue ball and keeping it blue. $$$$ Similarly, $E(3) = 1+\frac{3}{5}E(2)+\frac{2}{5}E(3)$, $E(2) = 1+\frac{3}{5}E(1)+\frac{3}{5}E(2)$, $E(1) = 1+\frac{1}{5}E(0)+\frac{4}{5}E(1)$. $E(0) = 0$, as if there are no red balls left, no more turns are needed. Solving this system of equations yields an answer for $E(5)$, which is what you want. $$$$ You could also use a Markov chain/matrix to find the expected value - this is pretty much the same thing.

Varun Vejalla
  • 8,873
1

enter image description here

I have posted a state diagram representing the game, as a hint. Hope this helps. If you're still not able to understand, please leave a comment and I'll be happy to help.

PS: The text in the circles represents the state we are in, i.e., how many balls have been colored blue. The number on the lines is the probability that we'll go to another state or stay in the same state.

Cheers!

Vizag
  • 3,257