What's going on with the behaviour of the subfactorial's imaginary part? Background: Out of curiosity I tried to construct some recurrence relations using the Pochhammer symbol and out of those came some subfactorials. For example:
$$a_{n+1}=a_n+(3)_n=a_n+3(3+1)(3+2)...(3+n-1).$$
Mathematica gave me:
$a_n$ = $1/2 (-1)^n$ Gamma[$n+3$] Subfactorial[$-n-3$]$-$Subfactorial[$-3$].
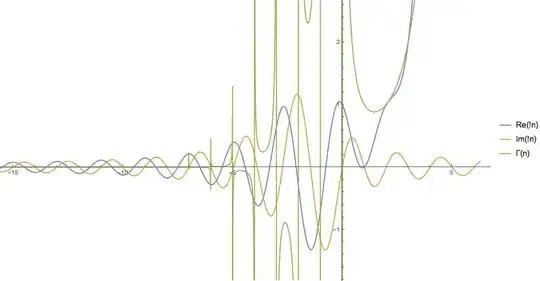
Not having seen seen negative subfactorials before I googled "negative subfactorial" or "subfactorial of negative numbers" and some similar phrases, which gave 0 hits. Here's a plot:
I also plotted the Gamma function (just to have something to relate to). So, I don't understand the behaviour of the imaginary part. Looking closer at the values of $\operatorname{Im}(!n)$ it appears that
$$\sum _{n=-\infty}^0 \operatorname{Im}(!n)=-\frac{\pi}{e^2}.$$
Anyone who can shed some light on this? Some intuition? Better methods of visualization?