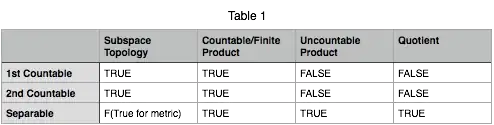
Hello, I made the following table to summarise the different countability properties. Im not quite sure if the values in the Uncountable product column are right. Any ideas?
Asked
Active
Viewed 39 times
0
-
Taking uncountable products doesn't preserve separability. For example, $\mathbb R^J$ is not separable when $|J|>2^{\omega}$. More details can be found on arbitrary product of separable spaces not always is separable – YuiTo Cheng Apr 10 '19 at 13:51
-
Its true if $J=|2^\omega|$ right? – Jhon Doe Apr 10 '19 at 14:01
-
Yes, $\mathbb R^{\mathbb R}$ is separable. – YuiTo Cheng Apr 10 '19 at 14:03
-
Hi just checking are the rest correct? – Jhon Doe Apr 10 '19 at 14:09
-
Yes, the remaining are fine. – YuiTo Cheng Apr 10 '19 at 14:11
-
Out of curiosity, why don't you include Lindelöf property in your list? It should enjoy the same status of other countability axioms. – YuiTo Cheng Apr 10 '19 at 14:17
-
As I go along i will be adding it. These are the properties that i have learned so far. – Jhon Doe Apr 10 '19 at 14:20
1 Answers
2
FYI: separability is hereditary for ordered spaces too, not just metrisable ones.
The uncountable case is a bit more subtle: yes for products with $\le \mathfrak{c}=2^{\aleph_0}$ factors, no for more (non-trivial) factors than that.
The rest of the table is fine.
In case you want to do Lindelöf: no for subspaces, except metrisable and ordered spaces again, already no for finite products (so certainly for more) and yes for quotients due to its being preserved by continuous images (like separable).
Henno Brandsma
- 242,131
-
Hello is it possible if you could show why separable ordered spaces have the separable property for its subspaces. I tried looking for proofs online but they seem to consider the isolated points of the subspace which is apparently countable and i can't see why. – Jhon Doe Apr 11 '19 at 08:35
-
@JhonDoe I gave the proof at "my" older forum here. It considers discrete subspaces as a lemma. Isolated points do play a role in the argument. – Henno Brandsma Apr 11 '19 at 21:36