1

Let $n>0$ and the probability for player $A$ to win a single game against $B$ be $p$.

A match consists of multiple independent games. What is the expected score-line of $A$ if the match ends when $A$ or $B$ wins $n$ games? (best-of-$(2n-1)$)

By simulation, it looks like below for $n=10$ and varying $p$, but whats the formula?

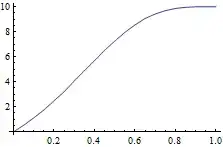Expected score for <span class=$n=10$ as a function of $p$.">

Sounds easy, but...

Help appreciated! Thanks in advance.

Eric Wofsey
  • 330,363
JHT
  • 360
  • What do you mean by "score line"? Are you just asking for the probability that $A$ wins the match? – lulu Apr 06 '19 at 20:11
  • Score line means the result e.g. 10-9, 10-1, or 8-10. For $A$ : 10, 10, 8. – JHT Apr 06 '19 at 20:15
  • Ok, well...the probability that $A$ wins the first $n$ is $p^n$. To get the probability that $A$ wins in exactly $n+1$ games, $A$ must win game $n+1$ and lose exactly one of the first $n$, hence $n\times (1-p)*p^n$. Can you finish from here? – lulu Apr 06 '19 at 20:17
  • But also scores where $A$ lost should contribute to the required expectation. – JHT Apr 06 '19 at 20:30
  • Yes, of course. That's why my expression has terms involving $(1-p)^i$. – lulu Apr 06 '19 at 20:36
  • Sorry, I meant when $A$ lost the match. – JHT Apr 06 '19 at 20:47
  • Well, it's easy to use the technique I described to compute the probability that $B$ wins in $n, n+1, \cdots$ games. – lulu Apr 06 '19 at 20:48
  • @lulu Is that what you had in mind? See below... – JHT Apr 06 '19 at 23:31
  • Well...to get expectation you need to weight by the number of games $A$ wins. I'd distinguish between the matches $A$ wins and those in which $B$ wins...for the first you have a term like $n\times p^n\times \sum_{i=0}^{n-1}\binom {n-1-i}i (1-p)^i$ and for the second you have $(1-p)^n\times \sum_{j=0}^{n-1}j\binom {n-1-j}jp^j$. – lulu Apr 06 '19 at 23:45

1 Answers1

0

Using this it follows

$E = \sum_{k=1}^{n} P(A$ wins $k$ games before $B$ wins $n)$

which gives

$E = \sum _{k=1}^n \sum _{j=k}^{n+k-1} \tbinom{k+n-1}{j} p^j (1-p)^{k+n-1-j}$.

This coincides with the simualations. Can we simplify that?

JHT
  • 360