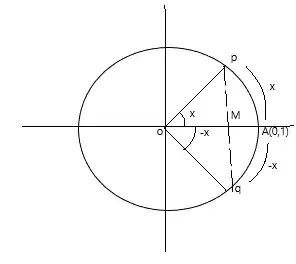
Ive been studying about opposite real number identities and Ive been stuck on this question on why $\cos(-x)=\cos x$. Okay so if we consider that the given circle is a unit circle and triangle $pom$ and triangle $qom$ are congruent then how $\cos(-x)=\cos x$?
According to me when we will do base/hypotenuse for triangle qom then it will come $om/oq$ which should give $-\cos x$ as $oq$ is negative, right?
Please help me through this.
$\cos x$ and $\sin x$ are respectively the abscissa and the ordinate of the point on the circle with angle $x$.
So, here, your points $p$ and $q$ have the same abscissa, so that $\cos x = \cos(-x)$. Note that they have opposite ordinates, so that $\sin(-x) = - \sin x$.
A non-geometry approach would be to consider the series definition for cosine. With this, for all $x\in\mathbb R$ the series $\sum_{n=0}^\infty\frac{(-1)^nx^{2n}}{(2n)!}$ converges and
$$\cos(x)=\sum_{n=0}^\infty\frac{(-1)^nx^{2n}}{(2n)!}.$$
For every $x\in\mathbb R$, you can now trivially see that
$$\cos(-x)=\sum_{n=0}^\infty\frac{(-1)^n(-x)^{2n}}{(2n)!}=\sum_{n=0}^\infty\frac{(-1)^n(-1)^{2n}x^{2n}}{(2n)!}=\sum_{n=0}^\infty\frac{(-1)^nx^{2n}}{(2n)!}=\cos(x)$$
Since you have already figured that $\triangle OMQ \cong \triangle OMP$, this means that the length of $OQ$ equals that of $OP$. In other words $|OQ|=|OP|$. Since they are congruent, their sides are equal in length and not opposite in sign.
Therefore by the identity
$$ \cos(\Theta)=\frac{\text{Adjacent}}{\text{Hypotenuse}}, $$
where the adjacent side might also be called the base. We have
$$ \cos(x)=\frac{|OM|}{|OP|}, $$ and $$ \cos(-x)=\frac{|OM|}{|OQ|}=\frac{|OM|}{|OP|}=\cos(x). $$
