1

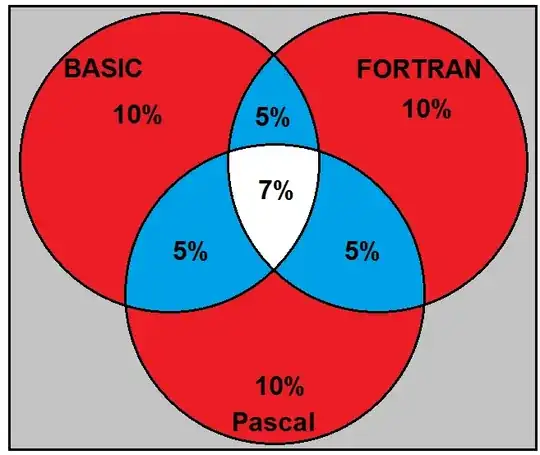
At one school, three computer languages, Basic, FORTRAN, and Pascal are taught. Suppose that for each language 27% of the students know that language, for each pair of languages 12% of the students know that pair of languages, and 7% of the students know all three languages. How many of the students do not know any computer language?

I am not sure how to start this but I think I use inclusion-exclusion method?

radius
  • 131
  • 5
  • This may help: https://math.stackexchange.com/questions/688019/what-is-the-inclusion-exclusion-principle-for-4-sets – NoChance Apr 02 '19 at 22:58

2 Answers2

0

Yup, inclusion/exclusion is at work here. Drawing a Venn diagram will prove particularly fruitful. Be mindful of intersections and what is in what: you should get something like this:

enter image description here

  • Since the intersection of two circles is $12\%$, we can conclude, since the intersection of all three is $7\%$, that the blue regions (the pairwise intersections excluding the intersection of all) is $12\% - 5\% = 7\%$

  • Similarly, since each circle has $27\%$ total, we subtract the blue/white regions of each circle to find that the red regions are $10\%$.

  • What we seek is the gray: those not accounted for by the circles. Sum up all the percentages from each region and subtract from $100\%$ to get the desired answer.

PrincessEev
  • 43,815
0

$n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A)-n(A \cap B \cap C)$

Using this formula, number of students not knowing any language can be obtained. Hope it helped you.

Divya Prakash Sinha
  • 456
  • This is close but there are 4 sets in the problem not only 3. See the comment I made up under the question. – NoChance Apr 03 '19 at 10:00