2

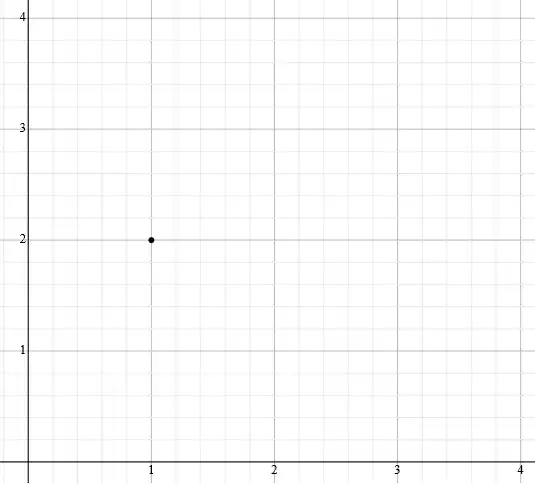
If the graph is only a point on the Coordinate plane, for example the graph of function

$f\left(x\right)=\left(x+1\right)$

Where the domain restricted to only {1} as the graph shows

The Domain restricted to only 1

How we can deal with this $\lim _{x\to 1}$?

is it impossible to find this ? or is it equal to 2 ?

Ammar Bamhdi
  • 143
  • This case is not covered by the old notion of limit in calculus, which is meaningfully defined only at accumulation points of the domain. – Sangchul Lee Mar 28 '19 at 16:30
  • Related: https://math.stackexchange.com/questions/942540/definition-of-functional-limits-and-isolated-points, https://math.stackexchange.com/questions/27429/why-not-define-limits-to-include-isolated-points, https://math.stackexchange.com/questions/267063/can-a-limit-of-a-function-thats-defined-only-in-one-point-exist, https://math.stackexchange.com/questions/1019388/why-are-punctured-neighborhoods-in-the-definition-of-the-limit-of-a-function – Hans Lundmark Mar 28 '19 at 17:05

1 Answers1

5

Using the usual concept of limit, which is$$\lim_{x\to a}f(x)=l\iff(\forall\varepsilon>0)(\exists\delta>0):0<\lvert x-a\rvert<\delta\wedge x\in D_f\implies\bigl\lvert f(x)-l\bigr\rvert<\varepsilon$$that limit can acutally be any number. However, usually one adds to the definition that $a$ must be a limit point of $D_f$, in which case the limit that you mentioned does not exist.

José Carlos Santos
  • 427,504