It is important to note that the flux $f(u)=-\frac13 u^3$ in the conservation law $u_t + f(u)_x = 0$ is nonconvex. The problem may be viewed as two neighbor Riemann problems, for which one can compute the waves, and their potential interactions. A plot of the base characteristic lines in the $x$-$t$ plane is given below:

One observes that the method of characteristics provides a unique solution $u = g(x + u^2 t)$ in some specific parts of the plane only. In facts, there may be zero, one or two characteristics passing at a given point $(x,t)$.
The previous plot suggest that a shock wave is generated at $x=0$, and that a rarefaction wave is generated at $x=1$. This claim is verified by convex hull constructions, a graphical method related to the Oleinik entropy condition for shock waves (see this post):
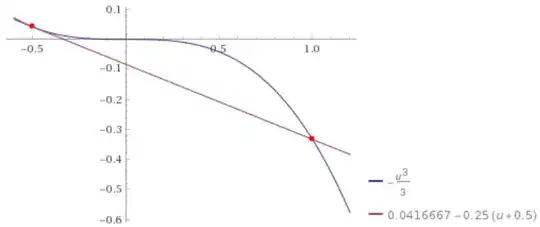
Here the Rankine-Hugoniot condition gives the shock speed $s = -\frac{1}{4}$. Hence, the following solution for times $t< \frac{4}{3}$ is obtained:
$$
u(x,t) = \left\lbrace
\begin{aligned}
&{-\tfrac12} & &\text{if}\quad x< {-\tfrac{1}{4} t}\\
&1 & &\text{if}\quad {-\tfrac{1}{4} t} < x \leq 1-t\\
&\sqrt{(1-x)/t} & &\text{if}\quad 1- t \leq x \leq 1-\tfrac14 t\\
&{\tfrac12} & &\text{if}\quad 1- \tfrac14 t \leq x
\end{aligned}
\right.
$$
For larger times, the interaction between the shock and the rarefaction must be computed.

