For an engineering application, I need the inverse functions of the computations of the number of combinations and permutations.
In the thread How to reverse the $n$ choose $k$ formula? it shows how to reverse/inverse the number of combinations function...
Given:
$X = C(n, k) = \binom{n}{k} = \frac{n! }{ k!(n-k)! }$
then you can limit n to:
$\sqrt[k]{k! X} + k \ge n \ge \sqrt[k]{k! X}$
And thus you at most need to check k+1 possible values of n (or with a binary search, just log(k+1) checks). Great!
But how do I solve for k instead of for n? (Given n and the number of combinations, how do I compute k?)
And given instead number of Permutations:
$X = P(n, k) = \frac{n! }{ (n-k)! }$
then I believe I am correct in assuming from above that:
$\sqrt[k]{X} + k \ge n \ge \sqrt[k]{X}$
And in this case, I actually can solve for k as well since k only appears once:
$k = n - InverseLnFactorial(ln(n!) - ln(X))$
And finally, given instead CR is Combinations with Repetitions:
$X = CR(n, k) = \binom{n+k-1}{k} = \binom{n+k-1}{n-1} = \frac{ (n+k-1)! }{ k!(n-1)! }$
then I believe I am correct in assuming from above that:
$\sqrt[k]{k! X} \ge n \ge \sqrt[k]{k! X} - k$
But again, how would I then solve for k instead of n? (Given n and the number of combinations with repetitions, how would I compute k?)
In both cases of Combinations (with and without repetitions), having k appear inside two different factorial terms makes it difficult for me to find an algebraic way to solve for k. Any help, or even clue, on how to do the algebra for those two cases would be greatly appreciated!

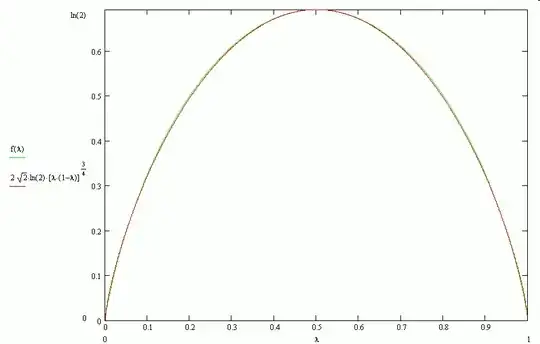
We know that $C(n,k)=\frac{n(n-1)\dots(n-k+1)}{1.2.3\dots k}$ To compute $k$ in $k$ steps, let $$ X_0=X \ X_1=\frac{X_0}{n}\ X_2=\frac{2X_1}{n-1}\ X_3=\frac{3X_2}{n-2}\ \vdots $$
If $X_i>1$, compute $X_{i+1}$. When $X_i=1$, we know that $k=i$ and $k=n-i$ are the desired solutions.
Reversing RC(n,k)
This time, $RC(n,k)=\frac{n(n+1)\dots (n+k-1)}{1.2.3\dots k}$. Let $$ X_0=X \ X_1=\frac{X_0}{n}\ X_2=\frac{2X_1}{n+1}\ X_3=\frac{3X_2}{n+2}\ \vdots $$
If $X_i>1$, compute $X_{i+1}$. When $X_i=1$, $k=i$ is the desired solution.
– Angela Pretorius May 19 '19 at 07:01