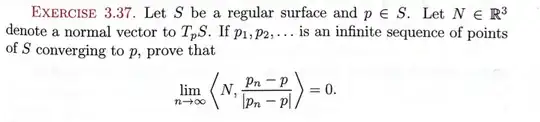It may very well be that $\lim_{n \to \infty} \frac{p_n-p}{|p_n-p|}$ does not exist. (To see this, consider an oscillation near a point.)
But by taking subsequences, we can prove the result, even if the limit above does not exist by itself. Fix a subsequence $p_{n_i}$ of $p_n$.
First, taking a parametrization $\varphi$ near $p$, we have that $p_{n_i}$ is in that chart for $i$ sufficiently big. Letting $q_{n_i}=\varphi^{-1}(p_{n_i})$, we know that
\begin{align}
\frac{p_{n_i}-p}{|p_{n_i}-p|}&=\frac{\varphi(q_{n_i})-\varphi(q)-d\varphi(q_{n_i}-q)+d\varphi(q_{n_i}-q)}{|q_{n_i}-q|}\cdot \frac{|p_{n_i}-p|}{|q_{n_i}-q|} \\
&=\frac{\varphi(q_{n_i})-\varphi(q)-d\varphi(q_{n_i}-q)}{|q_{n_i}-q|} +d\varphi\left(\frac{q_{n_i}-q}{|q_{n_i}-q|}\right)\cdot \frac{|p_{n_i}-p|}{|q_{n_i}-q|}.
\end{align}
By passing to subsequences yet again (twice), this converges to
$K\cdot d\varphi(h)$ for some $h \in \mathbb{R}^2$, $K \in \mathbb{R}$. Therefore, the limit of this subsequence $\frac{p_{n_{i_j}}-p}{|p_{n_{i_j}}-p|}$ of $p_{n_i}$ belongs to $T_pS$ and it follows that
$$\lim_{j \to \infty} \left\langle N, \frac{p_{n_{i_j}}-p}{|p_{n_{i_j}}-p|}\right\rangle=0.$$
Letting $a_n=\left\langle N, \frac{p_n-p}{|p_n-p|}\right\rangle$, we have thus proved that every subsequence of $a_n$ has a further subsequence converging to $0$. This proves that $a_n$ converges to zero. (This is a general fact about sequences - see here, for example.)