What is the probability that the nth card becomes the top card after shuffling a certain way?

Question

The following problem I can only seem to solve by simulation.

Suppose we take a deck and just label the cards from 1-52 in order, with 1 being the card on top. Now suppose we cut the deck at approximately the middle and complete the cut.

We could assume that there's an equal probability that we cut at each of 3 cards near the exact middle; that is, we either cut at exactly the middle (26 cards in hand), or we cut up to 29 cards or as few as 23 cards, all with equal probability.

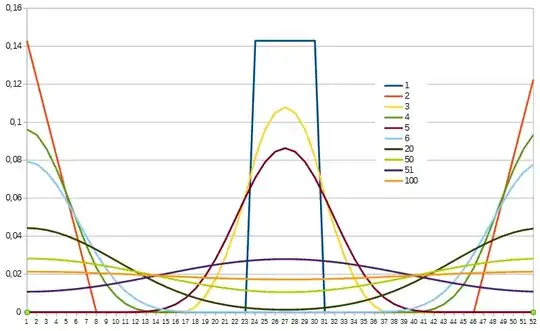
Then we could ask, what's the probability that the $n$th card is now on top? The answer is simply $0$ for most of the cards, and $\frac{1}{7}$ that cards 24, 25, 26, 27, 28, 29, or 30 are on top.

But suppose we perform this cut twice, what then? I think the simplest answer unfortunately is just to sum up all the ways you can make each outcome and total the probability. For example, obviously card #1 is most likely to return back on top after cutting twice. This can happen if you cut exactly in the middle twice, if you're short one and then long one, if you're short two and then long two, etc. In total, there is a $\frac{7}{49}$ chance card 1 is on top, a $\frac{6}{49}$ chance that card 2 is on top, etc.

I'm having trouble finding a general pattern here. If you have an odd number of cuts, the most likely cards are somewhere near the middle of the range 1-52; an even number of cuts and the most likely cards are near the edges. But how do I describe this mathematically?

Answer 1

For the first iterations you get a convolution of discrete uniform distribution (of $7$ values each), which will tend (for, say $n\approx 12$) to a Gaussian distribution with variance $4 n$ ($\sigma =2 \sqrt{n}$), alternatively centered around cards $27$ and $1$. Afterwards, there is a cyclic overlapping, so I don't think an analytic expression will be very simple (cf wrapped normal distribution).

You can solve this numerically by modelling it as a Markov chain with 52 states (positions).

Then, if $P$ is the transition matrix, the desired probabilities (after $n$ cuts) can be found in the first column of $P^n$.

For example, in Octave/Matlab

P = zeros(52,52);
for i=1:52
for k=23:29
  P(i,mod(i-1+k,52)+1) = 1/7;
endfor
endfor

P(:,1) % probabilities after the first cut
(P^2)(:,1) % probabilities after the second cut
(P^3)(:,1) % probabilities after the third cut...

Answer 2

One possibility is to put algebraic structure on the cards. They may be the elements $0,1,2,3,\dots, 51$ of the abelian group $\Bbb Z/52$ of the integers taken modulo $52$. Then let us start we $S_0=0$.

Completing a cut means adding to $S_0$ a random variable $X_1$ which is taking the values $26+k\in\Bbb Z/52$ for $k\in\{0,\pm1,\pm2,\pm3\}$ with equal probability $1/7$, and any other number with probability zero.

We can perform further cuts.

Then we add further random variables $X_2,X_3,\dots$ which have the same "shape" (repartition) as $X_1$. It is natural to write $X_k=26+Z_k$, so $Z_k$ takes values in $\{0,\pm1,\pm2,\pm3\}$ with probability one.

We have $S_0=0$, then

• $S_1=S_0+X_1=26+Z_1$ is "near" the middle $26$,
• $S_2=S_1+X_2=Z_1+Z_2$ is "near" the start $0$,
• $S_3=S_2+X_3=26+Z_1+Z_2+Z_3$ is "near" the middle $26$,
• $S_4=S_3+X_4=Z_1+Z_2+Z_3+Z_4$ is "near" the start $0$,

and so on. I would start the repartition of the process $(S_n)$ using this language...

Answer 3

There are seven possible cuts, each corresponding to a permutation of the cards, so each determining a $52\times 52$ permutation matrix. Let $P_1,P_2,\dots,P_7$ be these matrices. Let $M=\frac17(P_1+\dots+P_7)$. Finally, let $x$ be the $52\times 1$ column vector whose first coordinate is $1$ and whose other coordinates are zero. Then, the probability that card number $i$ is on top after $n$ cuts is just the $i^{th}$ coordinate of $M^nx$.