There are two closely related arrangements of the natural numbers that allow to show patterns in the distribution of some sets of numbers (multiples of 2, 4, 8, square numbers, prime numbers): the Archimedean spiral and the square spiral (Ulam-like).
[Click here to see an animated transition between these two arrangements.]
It turns out that some sets of numbers can be better grasped in the Archimedean spiral, others in the Ulam spiral (while this is subjective, I admit).
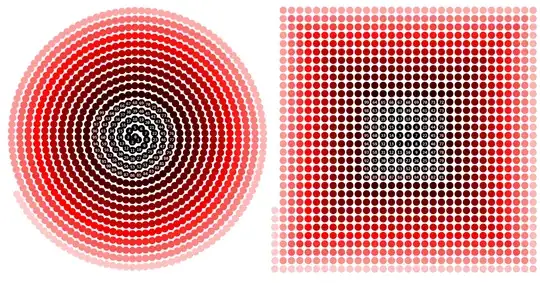
For example, a general pattern in the distribution of Euler's totient function can be slightly better seen in the Archimedean spiral (left) than in the Ulam spiral (right):
$\frac{\varphi(n)+1}{n}$ is depicted as shades of gray.
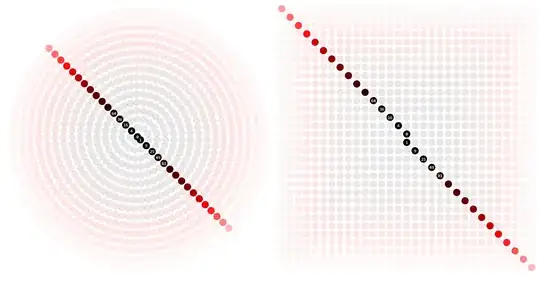
The prime numbers in turn – those with $\varphi(n)+1 = n$ – lie slightly more obviously on diagonals of the Ulam spiral than on any lines of the Archimedean spiral:
Other sets of natural numbers only look different (but regular in both spirals).
For example the even numbers:
Or the square numbers:
Or the multiplies of 4 and 8:
Or the "crystallographic defects" when highlighting those numbers with $\varphi(n) + 1 \leq \frac{n}{2}$ — compare with the numbers divisible by $2$ above:
Animated transitions for all the examples above can be seen here.
For those who want to play around: have a look here.
My question is:
Which bijective mapping of the plane – considered as $\mathbb{R}^2$ or $\mathbb{C}$ – does the transition from the Archimedean to the Ulam spiral correspond to?
Furthermore:
How can this mapping "explain" the commonalities and differences as observed above?
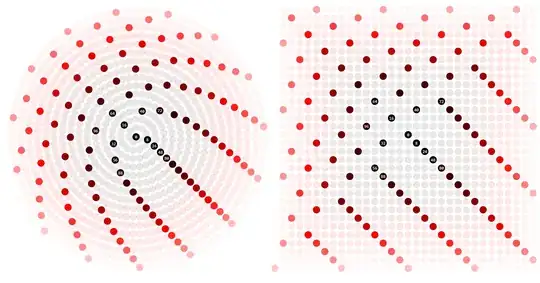
Addendum: To give you a better feeling how the mapping I'm looking for maps the points of the Ulam spiral to the points of the Archimedean spiral I created a "stream plot". The question is: What would be a closed expression for this mapping?