0

Here's the first part of the proof—the part I have a question about.

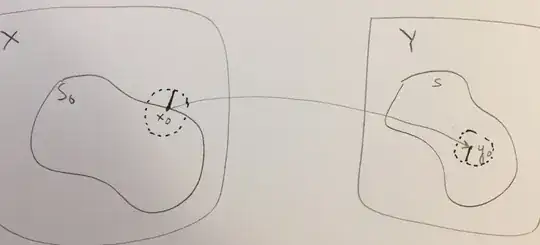
enter image description here

Simply put, I don't see anything here precluding $x_0$ from being on the boundary of $S_0$. And if that's the case then $N_0 \not\subset S_0$. Here's a picture of what's in my brain:

enter image description here

I'm sure that it's somehow implied $x_0$ can't be on the boundary but I'm not seeing it for some reason. Can someone please expand on the proof? Thank you.

Note: this is from Kreyszig's Introductory Functional Analysis with Applications.

Zduff
  • 4,252
  • This matters: what is your definition of continuity? The $\epsilon-\delta$ version? If so, there's your answer. – Randall Mar 17 '19 at 02:06
  • $S_0$ is open and $x_0$ belongs to $S_0,$ hence to the interior of $S_0$ and thus, is not in the frontier. – William M. Mar 17 '19 at 03:20

3 Answers3

2

The key part you are missing here is in the line

Since $T$ is continuous, $x_0$ has a $\delta$-neighborhood $N_0$ which is mapped into $\pmb N$.

Since $N$ is a subset of $S$, any subset of $\pmb X$ that is mapped into $\pmb N$ is a subset of $\pmb {S_0}$, since $S_0 = f^{-1}(S)$ is by definition the collection of points that get mapped into $S$. This is what forces the $\delta$-neighborhood to "not be on the boundary," since it must be wholly contained in $S_0$, by the definition of inverse image.

Alex Ortiz
  • 24,844
0

The $x_0$ drawn by you in the question is NOT an interior point (but a limit point). If you recall the definition of an open set (from a metric space perspective), it needs all points of the set to be interior points.

One additional note: this theorem helps to generalize the definition of continuous mapping from metric spaces into more generic topological spaces, where you no longer have concept of distance yet still have open sets.

UPDATE: so the question is actually about the other direction of the theorem.

Now let's pick any point in $X$, calling it $x_0$, $f(x_0) \in Y$. Let's say $f$ is continuous at point $x_0$, then $\forall \epsilon >0$, there exists $\delta_{\epsilon} > 0$, s.t. $\forall x \in A=\{x: |x - x_0| < \delta_{\epsilon} \}$, we have $B = f(A) \subset \{y: |y-y_0| < \epsilon\} \subset Y$.

Now you concern is: Why the point cannot be like what you drew (let's call it $x'$)?. Well, then for that $x'$ you drew, we cannot find a $\delta >0$ such that the above condition for continuity satisfies, and thus, $f$ is NOT continuous at the point $x'$ that you drew.

Jay Zha
  • 7,792
  • I'm not sure I understand. Aren't we trying to prove that $S_0$ is an open set? I'm confused as to why it's guaranteed that $x_0$ is not a boundary point of $S_0$. – Zduff Mar 17 '19 at 01:49
  • @Zduff it's because of the definition of continuity: you have a statement of the form $|x - x_0| < \delta$, which forces $x_0$ off the boundary. – Randall Mar 17 '19 at 02:08
  • @Zduff You are right, I was thinking about the other direction of the proof. I'll update – Jay Zha Mar 17 '19 at 02:15
0

I found this answer to be satisfying. The key part for me was that for any $x$ in the open $\delta$-ball around $x_0$ we have $Tx$ in the open $\epsilon$-ball around $Tx_0$, thus guaranteeing that all such $\delta$-balls are mapped into $S \subset Y$. Therefore every $x$ in such a $\delta$-ball must be in the inverse image of $S$. Furthermore, each of these $x$ are in an open set because each $\delta$-ball is open. Since $Tx_0$ was arbitrary, the result follows.

Zduff
  • 4,252