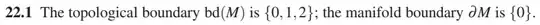Is $[0,1) \cup \{2\}$ a manifold with boundary? My issue is the $2$.

Question

• This has been asked about here: Understanding topological and manifold boundaries on the real line, and Sharkos said

Personally I'd say $M$ wasn't a valid manifold with boundary because the $\{2\}$ doesn't have a neighborhood with any structure like an open ball/half-ball.

• This is actually an exercise from An Introduction to Manifolds by Loring W. Tu and is not mentioned in an errata.

• I have spent almost 2 hours thinking about an exercise that looked like it would take only 15 minutes and even tried pasting lemma (it's a good thing Professor Tu has solutions unlike Professor Lee): The result of all that thinking is that I don't think $[0,1) \cup \{2\}$, $(\varepsilon,1) \cup \{2\}$ or $\{2\}$ is homeomorphic to any open subset of $\mathscr H^1$ or $\mathscr L^1$. I was able to show $\{0\} \subseteq \partial M$ and $(0,1)\subseteq M^0$, but I don't quite know where $2$ belongs. I believe $M$ is not locally $\mathscr H^1$.

• Also, I have double checked: I believe "manifold boundary" was defined for manifolds with boundary, so this isn't some trick where "manifold boundary" is actually defined for a Hausdorff and second countable space that need not be locally $\mathscr H^n$.

---

To generalize,

Is a half-open interval and a point not in the interval's closure a manifold with boundary?

Answer 1

The subset $[0,1[ \cup \{2\}$ of the real line is a manifold with boundary having two connected components of different dimensions. The component $[0,1[$ is a 1-dimensional manifold with boundary, and the single point {2} is a 0-dimensional manifold.

Answer 2

We need to refer to a definition of manifold with boundary.

Tu says

A topological $n$-manifold with boundary is a second countable, Hausdorff topological space that is locally ${\cal H}^n$.

where ${\cal H}^1 = [0,\infty)$ with the usual topology, and

We say that a topological space $M$ is locally ${\cal H}^n$ if every point $p \in M$ has a neighborhood $U$ homeomorphic to an open subset of ${\cal H}^n$.

Now consider $[0,1) \cup \{2\}$. Because of the line segment, it can only be a manifold with boundary if it is $n=1$ dimensional.

Now consider $p = 2$. Then every neighbourhood $U$ of $p$ contains an open set containing only one point. But no open set in ${\cal H}^1$ contains only one point. Hence $U$ cannot be homeomorphic to any subset of ${\cal H}^1$. Therefore, this is not a manifold with boundary.

---

As far as I can see, this isn't really open for debate given Tu's definitions (though perhaps I'm missing something!).

Edit: I should emphasize that it's fairly arbitrary whether one defines only "topological $n$-manifold" and "topological $n$-manifold with boundary", or if one generalizes to "topological manifold" and "topological manifold with boundary" where the $n$ can vary between different $p \in M$. As far as I can see, Tu does not actually define the latter notions.

If one does define these notions, then clearly this is a topological manifold which is a union of an $n=0$ manifold $\{2\}$ and a $n=1$ dimensional manifold with boundary $[0,1)$.