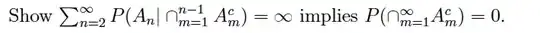2

enter image description here

This is what I am thinking:

Let $M< N <\infty $

$$P(\bigcap_{n=M}^N A_n^c) = \prod_{n=M}^N(1-P(A_n)) \leq \prod_{n=M}^N e^{(-P(A_n))}$$

$$= e^{\bigg( - \sum_{n=M}^N P(A_n)\bigg)} \rightarrow 0$$

as $N \rightarrow \infty$

So $$P(\bigcup_{n=M}^\infty A_n) = 1 \forall M$$ and since $$\bigcup_{n=M}^\infty A_n \downarrow \limsup A_n$$ it follows that

$$P(\limsup A_n) =1$$

So this statement would be the converse of what the question is asking right? Can someone please help me formulate this?

user477465
  • 720

1 Answers1

1

Independence is not required for this. Let $B_n=A_n\setminus (A_1\cup A_2\cup \cdots \cup A_{n-1})$. If possible let the conclusion be false. Then $c \equiv P (\cup_n A_n) <1$. It is easy to verify that the events $B_n$ are disjoint and their union is same as $\cup_n A_n$. Hence $\sum_n P(B_n)<1$. Now $\sum_n P(A_n|\cap_{k<n}A_k^{c}) \leq \sum_n \frac {P(B_n)} {1-P(A_1\cup A_2 \cup \cdots )}=\frac c {1-c} <\infty$.

Kavi Rama Murthy
  • 311,013
  • thank you, can you please explain what you mean by "if possible let the conclusion be false" ? Also why is $P(\cup_n A_n) < 1$? – user477465 Mar 12 '19 at 06:47
  • @user477465 We want to prove that $P(\cap A_n^{c})=0$. If this is false then $P(\cap A_n^{c})>0$. Taking complement we get $P(\cup A_n)<1$. – Kavi Rama Murthy Mar 12 '19 at 07:24