Is $|1-i|$ larger than $|1|$?

Question

I am confused about complex numbers. Does $1-i$ lie outside the unit circle? How do I show that the absolute value of $1-i$ is larger than that of $1$?

The question in the title made no sense, but the body of the post contained a different question which made sense. I've edited the title. — Asaf Karagila, Feb 26 '13 at 00:03
|a| = sqrt(C² + R²) => |1 - i| = sqrt(1² + 1²) = sqrt(2) and |1| = 1. sqrt(2) > 1 => |1 - i| > |1| — njzk2, Feb 26 '13 at 11:03

score 129 · Accepted Answer · edited Oct 15 '16 at 04:05

129

Let me do something very different for me. Let me give a geometric proof:

Note that $1-i$ is the bottom-right corner of the square whose center is $0$ and whose edges have length $2$. The other corners are $1+i; -1+i; -1-i$.

The diagonal running from $-1+i$ to $1-i$ is a straight line passing through $0$. Its length, by the Pythagoras theorem, is $2\sqrt2=\sqrt8$. Therefore the distance between $0$ and each of the corners is exactly half, i.e. $\sqrt2$.

And it is trivial to see that $\sqrt2>1$.

Here is a drawing:

$\hspace{5cm}$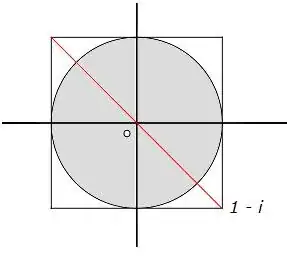 complex plane

edited Oct 15 '16 at 04:05

aduh

8,662

answered Feb 25 '13 at 23:04

Asaf Karagila

393,674

32

I must be very tired if I am thinking about this in terms of geometry. – Asaf Karagila Feb 25 '13 at 23:04
9

...and now I added a drawing. The horror... (If anyone can improve this drawing somehow, please do. :-)) – Asaf Karagila Feb 25 '13 at 23:18
Do you mean running from $- 1 + i$ to $1 - i$? – Feb 25 '13 at 23:21
@Andrew, that is what I mean. – Asaf Karagila Feb 25 '13 at 23:22
5

This is really the best demonstration of this property. +1 – Emily Feb 25 '13 at 23:38
10

+1 for being the only reasonable (read: geometric) answer! – Tyler Feb 26 '13 at 03:53
3

I concur, given the lack in intuitive understanding of complex numbers the OP showed, this really is the only reasonable answer. – Christian Feb 26 '13 at 10:06
@AsafKaragila : stop apologizing... Its a fantastic answer! – kumarharsh Feb 26 '13 at 12:33
@Peter: Awesomse!! – Asaf Karagila Feb 26 '13 at 16:06
1

@Harsh: Thanks, but I wouldn't normally have given such answer. Not geometric and not one illustrated. – Asaf Karagila Feb 26 '13 at 16:18
1

I only saw this answer now. How... atypical. ;) – J. M. ain't a mathematician Jun 02 '13 at 19:26
1

@Ｊ.M.: Why, yes! – Asaf Karagila Jun 02 '13 at 19:27
@AsafKaragila How did you draw the picture? – hola Jan 11 '15 at 12:22
1

@pushpen.paul: I used GIMP, and the basic geometric shapes. If you look at the history, though, you'll see that I didn't draw this image, but a much uglier one. This one was contributed by someone else with a bit more design skills than me. – Asaf Karagila Jan 11 '15 at 13:07
My dear Asaf: May I ask you to take a look at this answer? That is mine. Is that a wrong version? Thanks. – Mikasa Sep 14 '18 at 13:42
Indeed, th OP didn't have any attentions to it. – Mikasa Sep 14 '18 at 13:42

Git Gud · Answer 2 · 2019-05-22T23:01:10.330

45

By definition, the absolute value of a given complex number $z$ with $z=x+iy$ (for some $x,y\in \Bbb R$) is $\sqrt{x^2+y^2}$ and it is denoted by $|z|$.

If $z=1-i$, according to the definition we get $|1-i|=\sqrt{1^2+(-1)^2}=\sqrt {2}>1=|1|$.

edited May 22 '19 at 23:01

answered Feb 25 '13 at 22:45

Git Gud

31,356

Is this a violation of 7. from here ? – Maximilian Janisch May 22 '19 at 22:51
@MaximilianJanisch Yes. I evolved :) This is from 2013. I'll fix it. – Git Gud May 22 '19 at 23:00

Zev Chonoles · Answer 3 · 2013-02-25T22:50:36.050

33

Hint: By definition, if $a+bi$ is a complex number ($a$ and $b$ being real numbers, as usual), $$|a+bi|=\sqrt{a^2+b^2}.$$

Also, it is really incorrect to say that "$1-i$ is larger than $1$"; the complex numbers have no ordering. You should just instead say that $|1-i|>1$.

edited Feb 25 '13 at 22:50

answered Feb 25 '13 at 22:45

Zev Chonoles

129,973

score 15 · Answer 4 · answered Feb 25 '13 at 22:48

In complex number, you have to compute the module of a number to say if it is "larger" than something. In general the module is $$|a+bi|=\sqrt{a^2+b^2}$$

In your case $$|1-i|=\sqrt{1^2+(-1)^2}=\sqrt{2}$$

Then $$\sqrt{2}\geq|1|$$

And this imply that $1-i$ lies outside of the unit circle

score 10 · Answer 5 · answered Feb 25 '13 at 22:50

10

One of the properties of complex numbers is that we cannot compare them, but we can compare their modulus.

you can compare $|1-i|$ with $|1|$, equivalent with $\sqrt{1^{2}+1^{2}}\geq 1.$

answered Feb 25 '13 at 22:50

Iuli

6,790

score 5 · Answer 6 · edited Feb 26 '13 at 13:40

5

$|1|= 1$

$|1-i|= \sqrt{1^2+(-1)^2}=\sqrt{2}$

Since the modulus is radius in the Argand plane,

$|1-i|>|1|$

edited Feb 26 '13 at 13:40

answered Feb 26 '13 at 10:22

Inceptio

7,881

score 4 · Answer 7 · edited Feb 26 '13 at 11:31

4

Well as far as the title is concerned,

$|1-i|=\sqrt2$>$|1|$=1

$|1-i|$>$|1|$

edited Feb 26 '13 at 11:31

Inceptio

7,881

answered Feb 26 '13 at 09:08

IcyFlame

875

score 3 · Answer 8 · answered Sep 09 '14 at 14:01

This is a small variant of Asaf Karagila's geometric proof: If $a$ and $b$ are two points in the complex plane, the distance between them is $|a-b|$, so if you draw the (right isosceles) triangle with $a=1$, $b=i$ and $c=0$, you see that $|1-i|\gt1$.

score 1 · Answer 9 · edited Jan 25 '16 at 20:03

Here is another different approach:

The unique angle (in $[0,2\pi)$) between the vector $(1,i)$ in the complex plane and the x-axis is $\phi=\frac{7\pi}{4}$

Euler's identity yields now:

$$1-i=L(e^{\frac{7\pi}{4}i})=L\left(\cos\left(\frac{7\pi}{4}\right)+i\sin\left(\frac{7\pi}{4}\right)\right)=L\left(\cos\left(-\frac{\pi}{4}\right)+i\sin\left(-\frac{\pi}{4}\right)\right)=L\left(\cos\left(\frac{\pi}{4}\right)-i\sin\left(\frac{\pi}{4}\right)\right)=L\left(\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}\right) $$

Hence $L=\sqrt{2}$

Is $|1-i|$ larger than $|1|$?

9 Answers9