Why is it that (negative number) ^ (irrational number) is nonreal?

Question

We know that $(-1)^{\frac 12}$, $(-1)^{\frac 14}$, ... $(-1)^{\frac 1{even}}$ all result in complex answers, whereas $(-1)^{\frac 13}$, $(-1)^{\frac 15}$, ... $(-1)^{\frac 1{odd}}$ all result in real answers. I believe this comes from the definitions that $(-1)^{\frac 12} = \sqrt{-1} = i$ and $(-1)^{\frac 13}=\sqrt[3]{-1}=-1$. Moreover, of the set that provides real answers, if the numerator of the exponent is even, the result then becomes $+1$ instead of $-1$. This explains why the graph $y = (-1)^x$ results in an infinite amount of discontinuous points on $y=1$ and $y=-1$, only existing where the denominator of the exponent is odd:

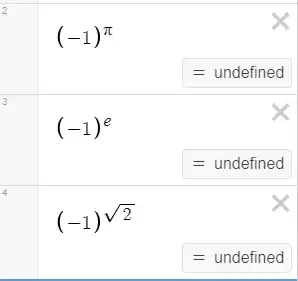
But the sets I provided only explain $(-1)^{rational}$; in other words, this assumes that we are only raising $-1$ to a fraction. When I plug in $(-1)^e$, $(-1)^{\pi}$, $(-1)^{\sqrt{2}}$, or any other irrational number, the answer comes back undefined/imaginary.

This cannot come from the explanation that I provided earlier because, even though it is the fundamental explanation for where imaginary results come from, it assumes the exponent is a fraction. My intuition is that there would be some other rule that would sometimes result in an imaginary answer and sometimes result in a real number - similar to how rational exponents work - but it seems to always be imaginary. What, then, is the rule for this, and can we prove that this is the case for all irrational numbers?

Answer 1

This is because the most general definition of $x^\alpha$ for complex $x,\alpha$ is $x^\alpha:=\exp(\alpha\log x)$, where $\exp$ is the exponential function and $\log$ is the (principal) natural logarithm. Pictorially, this means that taking $x$ to the power of $\alpha$ means multiplying the argument of $x$ by $\alpha$; that is, rotating $x$ with respect to the origin by an angle of $\alpha$ times the separation between $x$ and the positive real axis. So if $x$ is a negative real number and $\alpha$ is an irrational real number, then we must rotate $x$ by some irrational multiple of $\pi$ (i.e. $180^\circ$). Obviously, irrational numbers are never integers, so the result after the rotation never ends up on the real axis; that is, $x^\alpha$ is not real.

Answer 2

When we write $x^{\frac{1}{n}}$, this is just a notation. We mean to say that there should be a real number $y$ such that $y^n = x$. This definition is valid only when $n \in \mathbb{Z}$. But, when we want to do the same for irrationals, we do not have any definition. The usual intuition of exponents, which is multiplying the number itself as many times, will not work in case of irrationals. This is why we have to go into complex numbers where $w^z$ is defined for any complex numbers $w$ and $z$.

Answer 3

Every $z\in \mathbb{C}\setminus\{0\}$ can be written as $z=r\cdot e^{i\theta}$, with $r>0$ and $\theta\in\mathbb{R}$.

If $z$ is a negative real number, $r=-z$ and $\theta=(2n+1)\pi$, $n\in\mathbb{Z}$.

So, if $z^x=r^x\cdot e^{ix\theta}=(-z)^x\cdot e^{ix(2n+1)\pi}$ is real, then

$$(-z)^x\cdot e^{ix(2n+1)\pi} = r_0\cdot e^{ik\pi}$$ for some $r_0>0$ and $k\in\mathbb{Z}$. (Remember: $e^{ik\pi}=\pm1$, if $k\in\mathbb{Z}$)

So $ix(2n+1)\pi=ik\pi$ and then $x=\frac{k}{2n+1}\in\mathbb{Q}$.

In particular, if $x$ is irrational, so $z^x$ is not a real number

Answer 4

When considering $-1=e^{i\pi}$, the function $$f:\mathbb{R} \to \mathbb{C} \,\, ; \,\, x \mapsto (-1)^x=e^{i\pi x \, (\text{mod }2\pi)}=\cos(\pi x)+i\cdot \sin(\pi x)$$ becomes continuous. The expression $f(x)$ is real only if $x$ is an integer (you would need $\pi x$ to be equal to $\pi k$ for some integer $k$). Now this differs from the $n^{\text{th}}$-root concept you presented, for $(-1)^\frac{1}{3}=f(\frac{1}{3})=\frac{1}{2}+\frac{\sqrt{3}}{2}\cdot i \neq -1$. Also, with this you get $$f(\pi) \approx -0.9-0.43 \cdot i \,\,\,\, , \,\,\,\, f(e) \approx -0.633 +0.774 \cdot i$$

Answer 5

To answer, let us review Euler's identity.

If $e$ is the base of the natural logarithm, $i^2=-1$, then

$$e^{iπ}+1=0$$

As even powers of $-1$ are always equal to $1$, this implies that for all integers $z$

$$e^{i2πz}=(-1)^{2z}=1$$

Let $r$ be a real number, $n$ be an irrational number, and $H$ the measure of a half-circle. Applying a generalized version of Euler's formula:

$$(-r)^n=(e^{ln(-r)+i2πz})^n=(e^{ln(r)+iπ+i2πz})^n=(e^{ln(r)+iπ(2z+1})^n=e^{nln(r)+iπn(2z+1}=r^n\cos(Hn(2z+1)+ir^n\sin(Hn(2z+1)$$

Now, the zeroes of the sine function are integer multiples of a half-circle. $n$ being irrational and $2z+1$ being rational and always nonzero ($2z+1=0$ has no Diophantine solution), their product is irrational and the sine is always nonzero for all integers $z$, so the imaginary part can not vanish.

(fun fact: at least one of $r$, $n$, or $(-r)^n$ must be transcendental, per Gelfond-Schneider theorem)

Answer 6

As another responder said, $(-1)^{\frac m n}$ can be considered a process notation, meaning raise (-1) to the m-th power and then take the n-th root. This process does not at first glance seem to yield the values generated by the complex definition $(-1)^x = (e^{iπ})^x = e^{iπx}=\cos(πx)+i\sin(πx)$ for $x \notin \mathbb Z $.

For example:

• for $x={\frac 1 3}$ with the notation definition, $(-1)^{1/3} = -1$.
• using the complex definition, $(-1)^{1/3} = \cos({\frac 1 3}π)+i\sin({\frac 1 3}π) = {\frac 1 2}+i{\frac {\sqrt 3} 2}$.

However, using Euler's Equation, $e^{iπ}=-1$ can be generalized to $e^{i(2πk+π)}=-1$. If you choose k=1, then $e^{i(3π)}=-1$. The cube root of $e^{i(3π)}$ is $e^{iπ}$ or -1. In other words, in the complex model, there are 3 solutions for cube root, one of which is -1 (and the other 2 are complex, each ${\frac {2 \pi} 3}$ away from each other). If the exponent is rational, then there are a finite set of solutions, some of which will match the "notation solution(s)." If the exponent is irrational, the solutions will always be complex, never landing on $0{\pi}$ (for +1) or $1{\pi}$ (for -1) - and this corresponds to the fact that the "notation solution" doesn't produce a real number result for irrational exponents.

The apparent confusion could be compared to ${\sqrt 1}$. One person might get +1, and another -1. Both are valid and not in conflict. Also, even users of the "notation definition" would abide that ${\sqrt -1}={\pm}i$. This is the same thing. Here, the 2 results are $e^{{\frac \pi 2}i}$ and $e^{{\frac {3 \pi} 2}i}$ (which are ${\frac {2\pi} 2}$ apart).

As an aside, you could imagine other models for non-integer exponents. For example, you could define $(-1)^x = -(-1)\cos(πx)$. This produces an "intuitive" result where the values of $-1^x$ for $x \in \mathbb Z $ all match, and values for $x \notin \mathbb Z $ smoothly connect the matching points where $x \in \mathbb Z $. graph showing alternate model. Of course this wouldn't produce a mathematically consistent result and you'd have annoying issues like $e^a {\cdot} e^b {\neq} e^{a+b}$.

Finally, Euler's Equation itself depends on accepting that ${\sqrt -1}={\pm}i$. So, if you wish to bring chaos on math and reject that, you might find an alternate model for exponents!