Solutions of $\tan(x)=-\lambda x$?

Question

Motivated by a physical problem I would be interested in the solutions of $$\tan(x)=-\lambda x$$ with $\lambda,x \in \Bbb R^+$. Especially the first non-trivial solution (the trivial is $x=0$) would be of interest.

The problem with $\lambda=-1$ has some intriguing solutions, discussed here. So maybe there is a chance for a nice solution here as well? Nice shall not mean non-transcendental.

The methods from this link could maybe be modified?

Follow the links I give in my answer to $\tan(x) = x$. Find the values of $x$. For example, p. 13 of these conference slides indicate that it's probably not possible to find any reasonable explicitly expressed expressions for any of the nonzero solutions. — Dave L. Renfro, Mar 08 '19 at 18:24
Cool, thank you! Any chance you think for some special $|\lambda|<1$? — Raphael J.F. Berger, Mar 08 '19 at 18:31
I'm pretty sure the arguments involved (which I didn't provide, and I'm not even sure I could provide since I don't really know all that much about Schanuel’s Conjecture) would show that the conclusion is the same for any values of $\lambda$ that are themselves "reasonable explicitly expressed expressions", or even in the case of $\tan x = R(x)$ where $R(x)$ is a nonzero rational function all of whose coefficients are themselves "reasonably explicitly expressed expressions". (continued) — Dave L. Renfro, Mar 08 '19 at 18:43
Of course, it's easy by continuity arguments (specifically, using the intermediate value property of continuity) that there will exist values of $\lambda$ such that the least (strictly-) positive solution to $\tan x = {\lambda}x$ is equal to $42$ (or any other nice positive number of your choosing). My point is that any such $\lambda$ is probably not a number that has a "reasonable explicitly expressed expression". — Dave L. Renfro, Mar 08 '19 at 18:44
Not what you're looking after, surely, but for $\lambda >0$ the iteration $x_{n+1} = \tan^{-1}(-\lambda x_{n}) + \pi$ and (say) $x_0= \frac34 \pi $ converges quickly to the first non trivial root. — leonbloy, Mar 09 '19 at 22:18

score 1 · Accepted Answer · edited Jun 12 '20 at 10:38

Most has been already said in comments and answers.

If we think about approximations, we could notice that the function can be quite well represented by its $[2n,2n]$ Padé approximant built at $x=0$. For example, a simple one could be $$-\frac{\tan (x)}{x}\sim \frac{-1+\frac{1}{9}x^2-\frac{1}{945}x^4 } {1-\frac{4 }{9}x^2+\frac{1}{63}x^4 }$$ which shows an absolute error of $5.38\times 10^{-5}$ for $x=\frac{7\pi}{16}$ (using the next approximant, this error would become $7.24\times 10^{-9}$).

Then the approximation of the first root of $-\frac{\tan (x)}{x}=\lambda$ reduces to a quadratic (or cubic) equation in $x^2$.

Edit

If you have a look at this question of mine,we could work the problem slightly better considering the $[4,2]$ Padé approximant of $$\left(x-\frac{\pi }{2}\right) \left(x+\frac{\pi }{2}\right)\frac{ \tan (x)}{x}$$ This would lead to $$\frac{ \tan (x)}{x}=\frac{a_0+a_1x^2+a_2 x^4}{\left(x-\frac{\pi }{2}\right) \left(x+\frac{\pi }{2}\right) \left(1+a_3 x^2\right)}$$ where $$a_0=-\frac{\pi ^2}{4}\qquad a_1=\frac{-1680+140 \pi ^2+3 \pi ^4}{168 \left(\pi ^2-10\right)}$$ $$a_2=\frac{1680-180 \pi ^2+\pi ^4}{2520 \left(\pi ^2-10\right)}\qquad a_3=\frac{168-17 \pi ^2}{42 \left(\pi ^2-10\right)}$$ which is significantly better.

And here the circle closes, the Padé approximant obviuosly is another way of stating the perturbation theory https://theorie.ikp.physik.tu-darmstadt.de/tnp/pub/2009_padept_plb.pdf. — Raphael J.F. Berger, Mar 11 '19 at 18:53
@Rudi_Birnbaum. I was a quantum mechanicist and I worked this kind of approach in the very early 60's. — Claude Leibovici, Mar 12 '19 at 03:59

score 0 · Answer 2 · answered Mar 08 '19 at 18:37

0

For any $x \neq 0$, this is equivalent to $\lambda = \frac{-\tan(x)}{x}$. You can see a plot of this here. (For $x=0$, of course, it's satisfied by any $\lambda$ whatsoever.) But this probably isn't what you're asking.

For a given value of $\lambda$, on the other hand, this is significantly harder to solve. Dave L. Renfro in the comments points to page thirteen of these slides, which suggests that there is no "nice" non-trivial solution to $\tan(x) = R(x)$ for any nonzero rational function $R$. Unfortunately, $-\lambda x$ for any $\lambda \neq 0$ counts as a nonzero rational function.

This depends on Schanuel's conjecture, which hasn't been proven—but it's also unlikely to be disproven in a StackExchange answer. "Nice" here means "made of rational numbers and elementary functions".

answered Mar 08 '19 at 18:37

Draconis

1,443

The point is one can access single solutions of that type by what is called "perturbation theory" in physics. This could actually by the simplest possible example of a perturbation series. I might add something on that later in non-answer answer. – Raphael J.F. Berger Mar 08 '19 at 18:40
@Rudi_Birnbaum Interesting! I'm afraid I know nothing about perturbation theory, but if you can access solutions that way, you could write a more interesting answer. – Draconis Mar 08 '19 at 18:43
btw. as far as I am concerned I would be perfectly happy with an (nice) infinite series expression as well. – Raphael J.F. Berger Mar 08 '19 at 18:44
But the perturbation expansion will give infinite series containing with arbitrary high order of powers of π. Hope that's no spoiler, now. – Raphael J.F. Berger Mar 08 '19 at 20:19
@IV_ Thats a good idea, to try to sell it as an answer. My hope was actually that there could be a (more general) way how the coefficients can be expressed, before I post it as an answer. But here you go. – Raphael J.F. Berger Mar 10 '19 at 14:06
@IV_ as you see from my solution its about a general expression that contains $\lambda$ as a (continous) variable. That's what I'm after, and thats what the perturbation expansion does. – Raphael J.F. Berger Mar 10 '19 at 18:58

IV_ · Answer 3 · 2020-12-25T19:20:52.140

$$tan(x)=-\lambda x$$

$$\frac{tan(x)}{x}=-\lambda,\ \ x\neq 0$$

1.)
To solve this equation, you could use the partial inverses (= the branches of the inverse relation) of the elementary function $x\mapsto \frac{tan(x)}{x}$. It follows with Ritt's theorem on elementary inverse functions (1925) that the function doesn't have elementary partial inverses if its domain contains an open set. That means, it is not possible to solve the equation by only applying only elementary inverse operations of the elementary operations contained in the equation terms.

2.)
See this reference: Kheyfits, A. I.: Explicit solutions of transcendental equations and the Lambert W function. The author writes: "The method can be also applied to many other equations, like ... $w\ \tan w=z$ ..."
Apply this method to $\frac{tan(x)}{x}$, if this is possible.

Or use Lagrange inversion.

3.)
Let $T$ denote the inverse of the function $x\mapsto \frac{tan(x)}{x}$. Applying this to your equation above yields the solution $x=T(-\lambda)$.

4.)
For a given $\lambda$, you can use $\tan(x)+\lambda x=0$. The Taylor series of the function $x\mapsto \tan(x)+\lambda x$ is more simple than that of the function $x\mapsto \frac{\tan(x)}{x}$, and therefore its Lagrange inversion.

5.)
There is no elementary solution that you can read only from the equation. If you use a Special function or a series representation, e.g. a Taylor series, you have to calculate single values. The simplest way is therefore to calculate single values without using a formula for the partial inverses. Calculate a table of values of $x$ and $\frac{\tan(x)}{x}$ and invert this function. And apply the partial inverse functions to your $-\lambda$ as above.

6.)
Wolfram Alpha gives some numerical solutions. See e.g. here.

this function doesn't have an elementary inverse --- However, it should probably be pointed out that this fact doesn't prevent any (or even all) of the solutions to $\tan x = \lambda x$ from having "reasonable explicitly expressed expressions", such as Chow's notion of elementary number, Ritt's notion of elementary number (p. 60 of Ritt's Integration in Finite Terms, a Liouvillian number, etc. — Dave L. Renfro, Mar 09 '19 at 09:03

score 0 · Answer 4 · answered Mar 10 '19 at 14:03

Here is an outline how the problem can be tackled using perturbation theory on a quantum mechanical problem, that is directly related to it.

This is a graphical representation how the perturbation series approaches the exact curve for the first non-trivial non-negative root of (with swapped axis) $$\tan y = -x y$$ (this is the blue "exact" curve) the perturbation series is $$ u(c) = 1+c-c^2\frac{1}{4}+c^3\left(\frac{1}{16}-\frac{\pi^2-9}{48}\right)+c^4\left(-\frac{1}{64} +\frac{\pi^2-9}{192}-\frac{\pi^2-9}{96}+\frac{\pi^2-10}{64}\right) + \mathcal{O}(c^5) $$

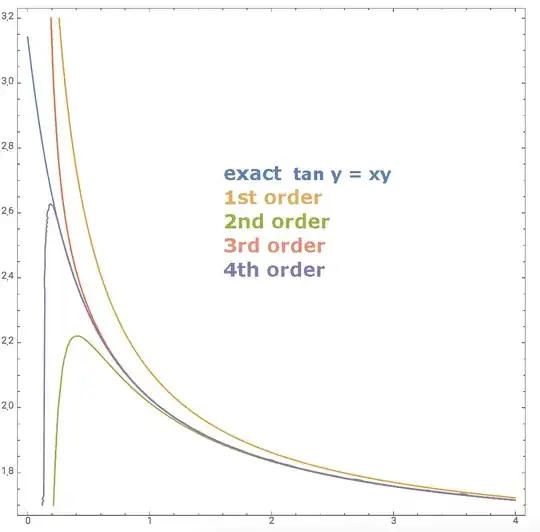The plot shows $$ y(x) = \frac{\pi}{2}\sqrt{u(c\left(\frac{8}{x\pi^2}\right))} $$ to order $n$ in $c^n$ (yellow: $1$ , green $2$, red $3$, purple $4$) and the exact curve $\tan y = xy$ (blue)

Solutions of $\tan(x)=-\lambda x$?

4 Answers4