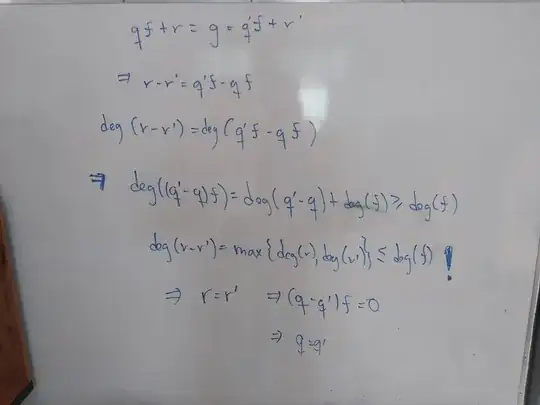2

Let $f(x), g(x) \in R[x]$ where $R$ is a domain, if the leading coefficient in $f(x)$ is a unit in $R$ then the division algorithm gives a quotient $q(x)$ and a remainder $r(x)$ after dividing $g(x)$ by $f(x)$. Prove that $q(x)$ and $r(x)$ are uniquely determined by $g(x)$ and $f(x)$.

I understand this Rotman exercise as a proof for the division algorithm for $R[x]$ where $R$, is a domain, I suppose it refers to an integer domain. But for the division algorithm for $f(x), g(x) \in R[x]$ where $R$ is a domain we don't use the fact $K$ is a field, just the fact that the leading coefficient in $f(x)$ is a unit in $R$ in the existence part. Im troubled because the hint for this exercise mention as a hint using $\operatorname{Frac}(R)$ so maybe I didn't understand what Im supposed to prove. Any help showing me what I'm supposed to prove and how to do it? Thanks

enter image description here

Bill Dubuque
  • 272,048
Cos
  • 1,799
  • If $c_f$, $c_g$ and $c_q$ are the leading coefficients of $f$, $g$ and $q$ respectively, then $c_g=c_qc_f$, and so it is necessary that $c_f$ divides $c_g$. If we assume that $c_f$ is a unit, this is certainly true. I think the hint suggests to first prove that the division algorithm yields unique $q(x)$ and $r(x)$ in $K[x]$, where $K=\operatorname{Frac}(R)$, and then prove that $q(x),r(x)\in R[x]$. – Servaes Mar 05 '19 at 20:16
  • Thanks but the problem is everybody is showing me how to prove uniqueness as if R[x] for R field but what is struggling me is that the nobody besides you mention the Hint. And I'm not sure how to use it in the proof @Servaes – Cos Mar 05 '19 at 20:40
  • I do not see how the hint is relevant in proving uniqueness either. All you need is that $$\deg\left((q-q')f\right)\geq\deg f,$$ which follows from the assumption that $R$ is a domain. – Servaes Mar 05 '19 at 20:49
  • Which Rotman book and what page? – Will Jagy Mar 05 '19 at 20:50
  • Advanced Modern Álgebra, page 142 , exercise 3,32 @WillJagy – Cos Mar 05 '19 at 20:54
  • I already post in my question an answer, is my proof right? Also the only fact I used is that K is an integer domain but I didn't use the fact the leading coefficient is an unit how is that? @ Servaes @Bernard – Cos Mar 05 '19 at 21:08
  • I think the fact in the hypothesis having the leading coefficient an unit is in order to proof the existence of q(x) and r(x) but this is not what I'm supposed to proof right? @ Servaes @Bernard – Cos Mar 05 '19 at 21:13
  • An ivertible coefficient is there to ensure the diivision is possible. It has nothing to do with uniqueness. Your proof is almost correct: what you really have is $\deg(r-r') <\deg f$, not $\le $. Otherwise you don't obtain a contradiction supposing $r-r'\ne 0$ (which you didn't say explicitly). – Bernard Mar 05 '19 at 21:14
  • Possibly Rotman's Hint aims to reduce the uniqueness proof to the case when the coef ring is a field, but that's more work than simply noting that the proof in the field case already works for divisors with unit lead coef (as in my answer). – Bill Dubuque Mar 05 '19 at 21:19
  • I agree that proving the existence of $q$ and $r$ is not part of the exercise; it seems to be assumed implicitly. In must emphasize that in your answer in the photo, the line $$\deg((q'-q)f)=\deg(q-q')+\deg(f)\geq\deg(f),$$ holds because $R$ is a domain and assuming that $q'-q\neq0$; this assumption is essential. Also note that $$\deg(r-r')\leq\max{\deg(r),\deg(r')},$$ and in general you need not have equality; the leading terms may cancel. – Servaes Mar 05 '19 at 23:32
  • @Servaes Please don't introduce notation that is inconsistent with the OP's textbook. I rolled it back and updated it to be consistent with Rotman. – Bill Dubuque Mar 05 '19 at 23:46
  • @BillDubuque Unfortunately I don't have the book at hand, so I didn't know which of the two indeterminates to use ($x$ or $X$). – Servaes Mar 05 '19 at 23:50
  • @Servaes I fixed that. All the $x$'s are lowercase now - as in Rotman. – Bill Dubuque Mar 05 '19 at 23:51

3 Answers3

1

If the exercise given to you is

Let $f(x), g(x) \in R[X]$ where $R$ is a domain, if the leading coefficient in $f(x)$ is a unit in $R$ then the division algorithm gives a quotient $q(x)$ and a remainder $r(x)$ after dividing $g(x)$ by $f(x)$. Prove that $q(x)$ and $r(x)$ are uniquely determined by $g(x)$ and $f(x)$.

then first of all there is a lot of sloppy notation; the symbols $x$ and $X$ are not interchangeable. Also, it seems to be implicit that $\deg r<\deg f$.

Second, it seems to be assumed that the division algorithm in $R[X]$ works, i.e. that it gives $q,r\in R[X]$ such that $g=qf+r$ and $\deg r<\deg f$. The question only asks to prove that these $q$ and $r$ are unique. That is to say, if $q',r'\in R[X]$ are such that $g=q'f+r'$ and $\deg r'<\deg f$, then $q'=q$ and $r'=r$.

To prove uniqueness, let $q,q,r,r'\in R[X]$ with $\deg r<f$ and $\deg r'<f$ be such that $$g=qf+r\qquad\text{ and }\qquad g=q'f+r'.$$ Then subtracting the two from eachother shows that $$(q-q')f=r'-r.$$ Of course $\deg(r'-r)<f$. Because $R$ is a domain, if $q-q'\neq0$ then $\deg\left((q-q')f\right)\geq\deg f$, a contradiction. Hence $q=q'$, from which it immediately follows that $r=r'$.

Note that this proof makes no use of the fraction field, but only of the fact that $R$ is a domain.

Servaes
  • 63,261
  • 7
  • 75
  • 163
0

Hint If $\, \deg r,\deg R < \deg\,f\,$ and $\,qf+r=Qf+R\,$ then $\,\color{#c00}{(Q−q)f}=\color{#0a0}{r−R}.\,$ If $\,Q\neq q\,$ then, by lead coef of $f$ is a unit, $\,\deg\rm \color{#c00}{LHS} \ge \deg f > \deg {\rm\color{#0a0}{ RHS}}\Rightarrow\!\Leftarrow\,$ So $\,Q=q\,$ so $\,r−R=0$

Bill Dubuque
  • 272,048
  • -1 This is incrediby hard to parse, and does not answer the question "What am I supposed to prove?". – Servaes Mar 05 '19 at 20:29
  • Thanks but what does LHS and RHS mean? And how I use the exercise hint here? – Cos Mar 05 '19 at 20:35
  • @Cos The red LHS refers to the matching red Left Hand Side of the equation (RHS is its Right Hand Side $= r-R$. The proof does not require any use of the fraction field. – Bill Dubuque Mar 05 '19 at 20:46
  • @cos If you're also interested in proving existence (not part of this exercise) then you can find a few ways here. That's what the (misplaced) Hint is aiming at. – Bill Dubuque Mar 05 '19 at 21:12
0

You're supposed to prove that if one can write \begin{cases}g(x)q(x)f(x)+r(x),\quad & r=0\;\text{ or }\;\deg r<\deg f,\\ g(x)q'(x)f(x)+r'(x),\quad & r=0\;\text{ or }\;\deg r'<\deg f \end{cases} in two ways, then $q=q'$ and $r=r'$.

Hint: deduce from these equalities that $$\bigl(q(x)-q'(x)\bigr)f(x)=r'(x)-r(x).$$ Suppose $r\ne r'$and compare the degrees of both sides.

Bernard
  • 175,478
  • Thanks! But I use the Hint telling me to use Fracc(R), here? @Bernard – Cos Mar 05 '19 at 20:38
  • No you make the proof again, taking into account the leading coefficient is a unit in $R$. You also can embed $R$ in its field of fractions $K$, hence $R[X}$ in $K[X]$, and use the uniqueness of Euclidean division for polynomial with coefficients in a field. – Bernard Mar 05 '19 at 20:43
  • @Cos We don't need to use the fraction Field (for existence) because Rotman already proves the monic case in Cor 3.22, so we can use this for monic $u^{-1}f$. But this is a moot point since the questions assumes existence is given. It concerns only uniqueness. The Hint is mistaken. – Bill Dubuque Mar 05 '19 at 20:52