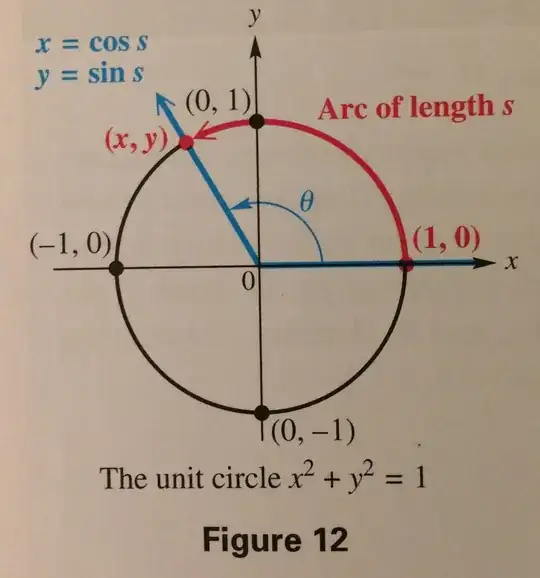
Upon introducing the idea of circular functions my textbook states:
We start at the point $(1,0)$ and measure an arc length $s$ along the circle. [...] Let the endpoint of this arc be at the point $(x, y)$. The circle is the unit circle - it has center at the origin and radius 1 unit (hence the name unit circle). Recall from algebra that the equation of this circle is: $x^2 + y^2 =1$
The radian measure of $\theta$ is related to the arc length $s$. For $\theta$ measured in radians, we know that $s=r\theta$. Here $r=1$, so $s$, which is measured in linear units such as inches or centimeters, is equal to $\theta$, measured in radians. Thus, the trigonometric functions of angle $\theta$ in radians found by choosing a point $(x, y)$ on the unit circle can be rewritten as functions of the arc length $s$, a real number. When interpreted this way, they are called circular functions.
I have several questions regarding this:
1) The text points out that the arc length, $s$ is measured in linear units while the angle measure, $\theta$, is in radians. Clearly two different units of measurement, so how could the two unit types be used interchangeably as the inputs of the trigonometric functions, where, for example, $\sin(s)= \sin(\theta)$?
2) $s=\theta$ is derived from $s=r\theta$ (formula for calculating arc length) and the fact that a unit circle has a radius of $1$, $r=1$. However, if the unit circle is not used and the radius is no longer 1, then is the arc length, $s$, still equal to the angle measure $\theta$? How?
3) Why not continue using angle measure in radians as the input for the trig. functions? Why use arc length instead?