This geometry problem comes from a recent math test.
The question is the following:
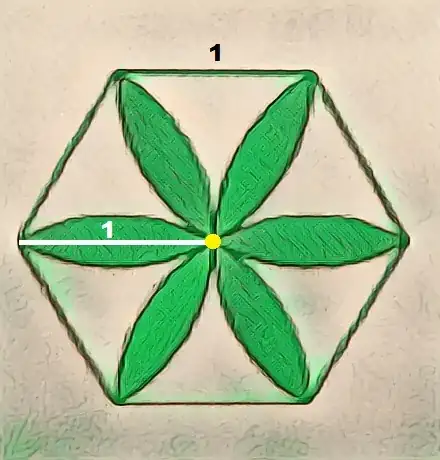
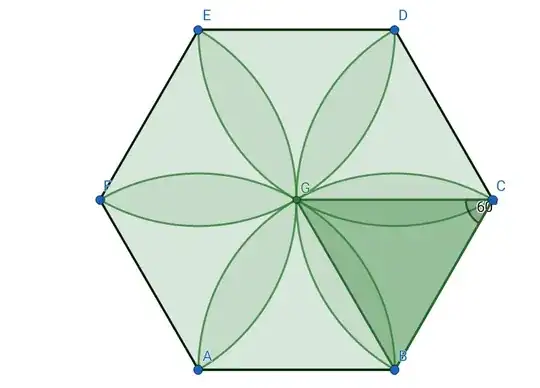
We have a regular hexagon with sides equal to $1$ and six circular arcs with radius equal to $1$ from each vertices of the hexagon in it creating a flower-shaped-like object. Find the area of the flower.
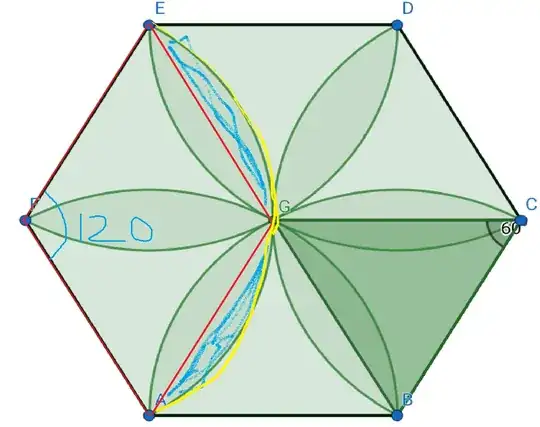
I tried creating an equilateral triangle by connecting the point in the center to the vertices of the boundary but was unable to proceed.
Would be thankful if you could help me out.
Assuming those are circular arcs and not "ellipses", you can indeed find the area exactly.
The "flower" has six "petals" Each of those petals has axial symmetry and can be divided into two halves. Each of those halves is the segment subtending a central angle of $\frac{\pi}{3}$ (radian measure) of a circle of radius $1$.
The area of one such segment is $\frac 12 r^2(\theta - \sin\theta) = \frac 12(\frac{\pi}{3} - \frac{\sqrt{3}}{2})$.
There are $12$ such segments, yielding the total area of the "flower" as $2\pi - 3\sqrt 3$.
Here's a solution that doesn't require trigonometry. The hexagon is made up of 6 "petals" and 6 "wedges" (the scooped out triangles between the petals). Call the area of a petal $p$, and the area of a wedge $w$.
What is the area enclosed by two adjacent sides of the hexagon and the arc drawn from the vertex between them? (For example, the region EFAGE). It's one third of a unit circle, and contains three petals and two wedges:
$3p + 2w = {\frac 1 3} \pi r^2 = \frac \pi 3$
What is the area of one triangle (one sixth of the hexagon)? The altitude of the triangle is $\sqrt{1 - {\frac 1 4}} = \frac{\sqrt 3}{2}$, so the area is $\frac{\sqrt 3}{4}$. The triangle is made up of two half-petals and one wedge:
$p + w = \frac{\sqrt 3}{4}$
Solving the two simultaneous equations:
$2p + 2w = \frac{\sqrt 3}{2}$
$p = \frac{\pi}{3} - \frac{\sqrt 3}{2}$
And the area of the flower is $6p = 2\pi - 3\sqrt 3$.
Shaded blue area is
(Area of pie)-(Area of rhombus)=$\pi\cdot 1^2\cdot\frac{120}{360}-1^2\cdot\sin(120)$=$ \frac{\pi}{3}-\frac{\sqrt{3}}{2}$
And we have 6 of them, and so total area of flower is
$ 6(\frac{\pi}{3}-\frac{\sqrt{3}}{2})=2\pi-3\sqrt{3}$
[This answer was posted for the original version of the problem, which had essentially no information about the figure other than the picture itself]
We can't easily find the area exactly - we just don't have enough information for that. But then, what are the estimates we're looking at? (1) $\approx 3.1$. (3) $\approx 4.7$. (4) $\approx 2.5$. (5) $\approx 3.3$. (6) $\approx 1.1$.
If the area's close to $3$, we might have difficulty deciding. If it's farther away, it'll be an easy choice.
Now, what's the area of the hexagon? That's something we can calculate exactly; an equilateral triangle of side $1$ has area $\frac{\sqrt{3}}{4}$, and the hexagon is six of those stuck together for a total area of $\frac32\sqrt{3}\approx 2.6$. The flower is clearly much less than that. Only one of the answers is plausible. It has to be (6), $2\pi-3\sqrt{3}$.
And, reverse-engineering from the answer... the curves that define the "petals" are the six circles centered at the vertices of the hexagon with radius $1$. That bit about "five ellipses" is just wrong.
Here's another way of looking at it. Imagine taking two circles of radius 1 and cutting them into thirds. Arrange them so that the six 120° angles you have (one from each wedge) form the corners of the hexagon.
Every point in one of the "petals" is covered by three of these wedges. Every point in the hexagon that's not in one of the petals is covered by two of these wedges. The total area covered by the six wedges is therefore twice the area of the total hexagon plus the area of the petals; or, in other words, the area of the petals is the area of two unit circles minus twice the area of the hexagon.
The area of the two circles is $2\pi$; the area of the hexagon is $3\sqrt{3}/2$. The area of the petals is therefore $2 \pi - 3 \sqrt{3} \approx 1.087...$
