1

Given

  1. $f:\mathbb R \to \mathbb R$

  2. $f$ is continuous

  3. $f(f(x))=x$

Find $f(x)$.

I only find $f(x)=x$ and $f(x)=a-x$. Are there other solutions? Thank you.

Community
  • 1
JSCB
  • 13,456
  • 15
  • 59
  • 123
  • 2
    f(x)=a-x is one obvious solution. There are many(infinitely many) more. – Ishan Banerjee Feb 24 '13 at 07:05
  • 2
    $f(x)=a/x$ satisfy if $x \neq 0$. – JSCB Feb 24 '13 at 07:06
  • @jasoncube: Since $0\in\Bbb R$, your example $f(x)=a/x$ doesn't quite work, but it's good that you're thinking about the problem! – Clayton Feb 24 '13 at 07:09
  • @ Ishan Banerjee: For example? – JSCB Feb 24 '13 at 07:10
  • 2
    You haven't demanded that the function be continuous; just that it be from reals to reals. So a function $f$ where $f(x)=a/x$ when $x\neq0$ will be OK, if you further specify that $f(0)=0$. The bigger picture that Ishan may be getting at, is that since you are not requiring $f$ to be continuous, you really have a lot of freedom to make up functions that satisfy this. For example, $f(x)=x$ for $x$ other than $1,2$, with $f(1)=2$ and $f(2)=1$. – 2'5 9'2 Feb 24 '13 at 07:12
  • Oh, let me restrict it a bit. – JSCB Feb 24 '13 at 07:19
  • 6
    OK, now take any continuous function whose graph is symmetric across the line $y=x$. That is, imagine any graph that you can such that when $(a,b)$ appears on the graph, then so does $(b,a)$. These functions also work: $f(f(a))=f(b)=a$. For an example that demonstrates how complicated the curve could be, take the graph of $y=\cos(x)$ and rotate it 45 degrees clockwise about the origin. – 2'5 9'2 Feb 24 '13 at 07:25
  • 1
    Related: http://math.stackexchange.com/questions/46635/examples-of-involutions-on-mathbbr – Ink Feb 24 '13 at 07:42
  • For some simple explicit examples, take $x^2 + y^2 + a x y = 1$ for $a > 2$. – Robert Israel Feb 24 '13 at 09:16
  • The only increasing function satisfying the equation $f(f(x))＝x$ is $f(x)＝x$. Indeed, suppose $f(a)<a$ for some $a$. Since $f$ is increasing, taking $f$ to both sides give $a＝f(f(a))<f(a)$, a contradiction. Similar argument allows us to exclude the possibility that $f(a)>a$ for some $a$. But as discussed both above and below, there are infinitely many continuous decreasing solutions. – Sangchul Lee Feb 25 '13 at 08:51

2 Answers2

8

There are infinitely more continuous solutions.

In fact, let $g$ be any continuous bijection from $\mathbb{R}$ back to itself, then the map defined by:

$$\mathbb{R} \ni x \;\overset{f}{\longrightarrow}\; g^{-1}(-g(x)) \in \mathbb{R}$$

is continuous and for all $x$, satisfies:

$$f(f(x)) = g^{-1}(-g(g^{-1}(-g(x))) = g^{-1}(-(-g(x)) = g^{-1}(g(x)) = x$$

For example, if one take $g(x) = x - \frac{a}{2}$, you get

$$g^{-1}(-g(x)) = \left(-\left(x - \frac{a}{2}\right)\right) + \frac{a}{2} = a - x$$

If you take something more crazy like $g(x) = x^3 - a/2$, you get:

$$g^{-1}(-g(x)) = \left(-\left(x^3 - \frac{a}{2}\right) + \frac{a}{2}\right)^{\frac13} = (a - x^3)^{\frac13}$$

A very strange looking curve but still a continuous solution for the equation $f(f(x)) = x$.

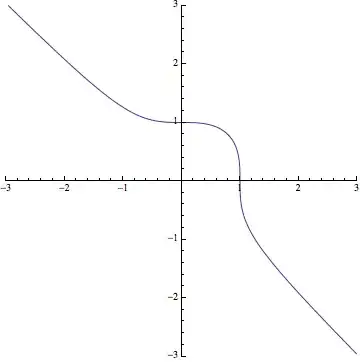
$y = (1-x^3)^{1/3}$

Credit above graph comes from $\mathbb{R}^n$ which exhibit the $x \leftrightarrow y$ symmetry explicitly.

achille hui
  • 122,701
  • Here is the same graph with a 1:1 aspect ratio, if you want to include in your answer. –  Feb 25 '13 at 08:07
  • @Rn, thanks for the graph. – achille hui Feb 25 '13 at 08:41
  • Can we find a function $f$ defined on $\Bbb{R}$ such that $(f\circ f)(x)=-x$ ? It seems that such a function is not continuous. –  May 30 '15 at 20:41
  • 1
    @Gato For non-continuous $f$, yes. Partition the positive numbers into pairs $\mathbb{R}{+} = \bigcup{i\in I} { u_i, v_i }$. If you define $f$ as $$f(x) = \begin{cases} 0, & x = 0\ v_i, & \text{ if } x = u_i \text{ for some } i \in I\ -u_i & \text{ if } x = v_i \text{ for some } i \in I\ -f(-x)& x < 0 \end{cases} $$ then $f(f(x)) = -x$ – achille hui May 30 '15 at 20:51
  • @achillehui You are an erudite person, nice way. Thanks –  May 30 '15 at 20:55
3

If I were allowed to impose more strict condition

ii. $f$ is differentiable

then $f(x) = x$ and $f(x) = a - x$ are the only solutions.

From condition 3, we get ODE (f'(x))^2 = 1 $f'\big(f(x)\big)f'(x) = 1$. If $f' \equiv 1$ then $f(x) = a + x$. And $x = f(f(x)) = 2a + x$ shows $a = 0$. Otherwise If $f' \equiv -1$ then $f(x) = a - x$. And $x = f(f(x)) = x$ shows arbitrary constant $a$ is allowed.

Edit: As @ChristianBlatter points out to me, I made a big mistake. I correct the error but this answer becomes almost worthless.

Orat
  • 4,065