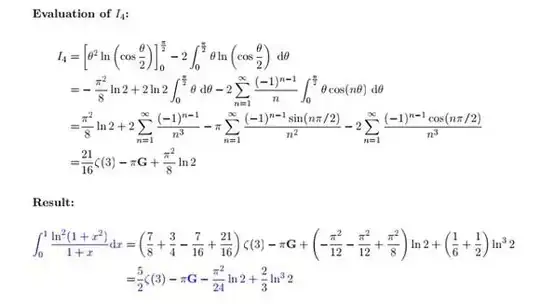How to evaluate $\int_{0}^{1}{\frac{x\ln(1+x)\ln(1+x^2)}{1+x^2}}dx$

Question

How to evaluate $$\int_{0}^{1}{\frac{x\ln(1+x)\ln(1+x^2)}{1+x^2}}dx$$

My attempt

$$\begin{align}\int_{0}^{1}{\frac{x\ln(1+x)\ln(1+x^2)}{1+x^2}}dx&=\frac{1}{4}\int_{0}^{1}{\ln(1+x)}d(\ln^2(1+x^2))\\ &=\frac{1}{4}(\ln(1+x)\ln^2(1+x^2)|_0^1-\int_{0}^{1}{\ln^2(1+x^2)}d\ln(1+x))\\ &=\frac{1}{4}(\ln^32-\int_{0}^{1}\frac{\ln^2(1+x^2)}{1+x}dx)\\ \end{align}$$

$$\begin {align} &\int_{0}^{1} \frac{\ln ^{2}\left(1+x^{2}\right)}{1+x} d x\\=&\int_{0}^{1} \frac{\ln ^{2}\left(1-y^{2}\right)}{1+i y} i d y-\int_{0}^{\frac{\pi}{2}} \frac{\ln ^{2}\left(1+e^{i 2 \theta}\right)}{1+e^{i \theta}} i e^{i \theta} d\theta\\ =&\int_{0}^{1} \frac{y \ln ^{2}\left(1-y^{2}\right)}{1+y^{2}} dy+\frac{1}{2} \int_{0}^{\frac{\pi}{2}} \tan \left(\frac{\theta}{2}\right) \ln ^{2}(2 \cos \theta)d\theta+\int_{0}^{\frac{\pi}{2}} \theta \ln (2 \cos \theta)d\theta\\&-\frac{1}{2} \int_{0}^{\frac{\pi}{2}} \theta^{2} \tan \left(\frac{\theta}{2}\right)d\theta \end {align}$$

But how to evaluate $$\int_{0}^{1}\frac{\ln^2(1+x^2)}{1+x}dx$$

The answer from Mathematica is $$\frac{1}{96}(24\pi\mathbf{G}+\pi^2\ln2+8\ln^32-60\zeta(3))$$

$\mathbf{G}$ is Catalan's constant.

My answer

Answer 1

You already used contour integration to split the integral into four parts: $$\begin {align} &\int_{0}^{1} \frac{\ln ^{2}\left(1+x^{2}\right)}{1+x}dx\\ =&\int_{0}^{1} \frac{x \ln ^{2}\left(1-x^{2}\right)}{1+x^{2}} dx+\frac{1}{2} \int_{0}^{\pi/2} \tan \left(\frac{x}{2}\right) \ln ^{2}(2 \cos x)dx+\int_{0}^{\pi/2} x \ln (2 \cos x)dx\\&-\frac{1}{2} \int_{0}^{\pi/2} x^{2} \tan \left(\frac{x}{2}\right)dx \end {align}$$

---

Denote those four integrals by $I_1,\cdots, I_4$. $$I_1 = \frac{1}{2}\int_0^1 \frac{\ln^2(1-x)}{1+x}dx = \frac{1}{2}\int_0^1 \frac{\ln^2(x)}{2-x}dx = \text{Li}_3(\frac{1}{2}) = \frac{\ln^2 3}{6}-\frac{\pi^2}{12}\ln 2 +\frac{7}{8}\zeta(3)$$ For $I_2$, tangent-half substitution gives $$I_2 = \int_0^1\frac{2t\ln^2(2\frac{1-t^2}{1+t^2})}{1+t^2}dt = \int_0^1 \frac{\ln^2(2\frac{1-t}{1+t})}{1+t}dt = \int_0^1 \frac{\ln^2 (2t)}{1+t}dt = \frac{3\zeta(3)}{2}+\ln^3 2 -\frac{\pi^2}{6}\ln 2$$ where the penultimate step involves $t\mapsto (1-t)/(1+t)$.

For $I_3$, integration by part gives $$I_3 = \int_0^{\pi/2} (\frac{\pi}{2}-x)\ln(2\sin x) dx = -\frac{\pi^2}{8}\ln 2+\frac{1}{2}\int_0^{\pi/2} x^2 \cot x dx $$ Use the identity $$\sum_{n=1}^N \sin(nx) = \frac{1}{2}\cot\frac{x}{2}-\frac{\cos(N+1/2)x}{2\sin(x/2)}$$ letting $N\to \infty$, and the remainder $\to 0$ by Riemann-Lebesuge lemma, so $$\int_0^{\pi/2} x^2\cot x dx = 2\sum_{n=1}^\infty \int_0^{\pi/2} x^2\sin(2nx) dx = \frac{\pi^2}{4}\ln 2 -\frac{7\zeta(3)}{8}$$ Note that each summand can be evaluated explicitly. Therefore $I_3 = -7\zeta(3)/16$.

For $I_4$, use the same identity, gives $$I_4 = 2\sum_{n=1}^\infty \int_0^{\pi/2} x^2\sin[n(\pi-x)]dx = 2\sum_{n=1}^\infty (-1)^{n+1} \int_0^{\pi/2} x^2\sin (nx)dx$$ the series definition of Catalan constant immediately gives $$I_4 = 2\pi G - \frac{21\zeta(3)}{8} - \frac{\pi^2}{4}\ln 2$$

Combining all these should give you the result.

Answer 2

An alternative "elementary" solution (no contour integral, no complex number actually)

Hold your breath !

\begin{align}\text{A}&=\int_0^1 \frac{x\ln(1-x)\ln(1+x^2)}{1+x^2}\,dx\\ \text{B}&=\int_0^1 \frac{x\ln(1+x)\ln(1+x^2)}{1+x^2}\,dx\\ \text{A+B}&=\int_0^1 \frac{x\ln(1-x^2)\ln(1+x^2)}{1+x^2}\,dx\\ \end{align}

Perform the change of variable $\displaystyle y=x^2$,

\begin{align} \text{A+B}&=\frac{1}{2}\int_0^1 \frac{\ln(1-x)\ln(1+x)}{1+x}\,dx\\ &=\frac{1}{4}\int_0^1 \frac{\ln^2(1-x)}{1+x}\,dx+\frac{1}{4}\int_0^1 \frac{\ln^2(1+x)}{1+x}\,dx-\frac{1}{4}\int_0^1 \frac{\ln^2\left(\frac{1-x}{1+x}\right)}{1+x}\,dx\\ &=\frac{1}{4}\int_0^1 \frac{\ln^2\left(\frac{2x}{1+x}\right)}{1+x}\,dx+\frac{1}{4}\int_0^1 \frac{\ln^2(1+x)}{1+x}\,dx-\frac{1}{4}\int_0^1 \frac{\ln^2 x }{1+x}\,dx \end{align}

In the first and the third integral perform the change of variable $y=\dfrac{1-x}{1+x}$,

\begin{align} \text{A+B}&=\frac{1}{4}\int_0^1 \frac{\ln^2\left(\frac{2x}{1+x}\right)}{1+x}\,dx+\frac{1}{4}\int_0^1 \frac{\ln^2(1+x)}{1+x}\,dx-\frac{1}{2}\int_0^1 \frac{\ln^2 x }{1+x}\,dx\\ &=\frac{1}{4}\int_0^1 \frac{\ln^2(1+x)}{1+x}\,dx-\frac{1}{2}\int_0^1 \frac{\ln(1+x)\ln x}{1+x}\,dx-\frac{\ln 2}{2}\int_0^1 \frac{\ln(1+x)}{1+x}\,dx\\ &+\frac{1}{4}\int_0^1 \frac{\ln^2 x}{1+x}\,dx+\frac{\ln 2}{2}\int_0^1 \frac{\ln x}{1+x}\,dx+\frac{\ln^2 2}{4}\int_0^1 \frac{1}{1+x}\,dx+\frac{1}{4}\int_0^1 \frac{\ln^2(1+x)}{1+x}\,dx-\\ &\frac{1}{4}\int_0^1 \frac{\ln^2 x }{1+x}\,dx\\ &=\frac{1}{6}\ln^3 2-\frac{1}{2}\int_0^1 \frac{\ln(1+x)\ln x}{1+x}\,dx+\frac{1}{2}\ln 2\int_0^1 \frac{\ln x}{1+x}\,dx \end{align}

\begin{align} \text{A-B}&=\int_0^1 \frac{x\ln\left(\frac{1-x}{1+x}\right)\ln(1+x^2)}{1+x^2}\,dx\\ \end{align}

Perform the change of variable $y=\dfrac{1-x}{1+x}$

\begin{align} \text{A-B}&=\int_0^1 \left(\frac{1}{1+x}-\frac{x}{1+x^2}\right)\ln\left(\frac{2(1+x^2)}{(1+x)^2}\right)\ln x\,dx\\ &=\ln 2\int_0^1 \frac{\ln x}{1+x}\,dx-\ln 2\int_0^1 \frac{x\ln x}{1+x^2}\,dx+\int_0^1 \frac{\ln x\ln(1+x^2)}{1+x}\,dx-\int_0^1 \frac{x\ln x\ln(1+x^2)}{1+x^2}\,dx-\\ &2\int_0^1 \frac{\ln x\ln(1+x)}{1+x}\,dx+ 2\int_0^1 \frac{x\ln x\ln(1+x)}{1+x^2}\,dx\\ \end{align}

In the second and the fourth integrals perform the change of variable $\displaystyle y=x^2$,

\begin{align} \text{A-B}&=\frac{3}{4}\ln 2\int_0^1 \frac{\ln x}{1+x}\,dx+\int_0^1 \frac{\ln x\ln(1+x^2)}{1+x}\,dx-\frac{9}{4}\int_0^1 \frac{\ln x\ln(1+x)}{1+x}\,dx+ 2\int_0^1 \frac{x\ln x\ln(1+x)}{1+x^2}\,dx\\ \end{align}

Define function $R$ on $[0;1]$ by:

\begin{align}R(x)&=\int_0^x \frac{\ln t}{1+t}\,dt\\ &=\int_0^1 \frac{x\ln(tx)}{1+tx}\,dt\\ \end{align}

Therefore,

\begin{align} \text{C}&=\int_0^1 \frac{\ln x\ln(1+x^2)}{1+x}\,dx\\ &=\Big[R(x)\ln(1+x^2)\Big]_0^1 -\int_0^1 \int_0^1 \frac{2x^2\ln(tx)}{(1+tx)(1+x^2)}\,dt\,dx\\ &=\ln 2\int_0^1 \frac{\ln x}{1+x}\,dx-\int_0^1 \int_0^1 \frac{2x^2\ln t}{(1+tx)(1+x^2)}\,dt\,dx-\int_0^1 \int_0^1 \frac{2x^2\ln x}{(1+tx)(1+x^2)}\,dt\,dx\\ &=\left(\int_0^1 \frac{2t\ln t\ln(1+t)}{1+t^2}\,dt-\int_0^1 \frac{2\ln t\ln(1+t)}{t}\,dt-\int_0^1 \frac{(\ln 2) t\ln t}{1+t^2}\,dt+\frac{\pi}{2}\int_0^1 \frac{\ln t}{1+t^2}\,dt\right)-\\ &\int_0^1 \frac{2x\ln x\ln(1+x)}{1+x^2}\,dx+\ln 2\int_0^1 \frac{\ln x}{1+x}\,dx\\ &=\ln 2\int_0^1 \frac{\ln x}{1+x}\,dx-2\int_0^1 \frac{\ln t\ln(1+t)}{t}\,dt-\ln 2\int_0^1 \frac{ t\ln t}{1+t^2}\,dt-\frac{1}{2}\pi\text{G} \end{align}

(all the integrals have been computed using antiderivatives)

In the third integral perform the change of variable $\displaystyle y=t^2$,

\begin{align} \text{C}&=\frac{3}{4}\ln 2\int_0^1 \frac{\ln x}{1+x}\,dx-\Big[\ln^2t\ln(1+t)\Big]_0^1+\int_0^1 \frac{\ln^2 t}{1+t}\,dt-\frac{1}{2}\pi\text{G}\\ &=\frac{3}{4}\ln 2\int_0^1 \frac{\ln x}{1+x}\,dx+\int_0^1 \frac{\ln^2 t}{1+t}\,dt-\frac{1}{2}\pi\text{G}\\ \end{align}

Define function $S$ on $[0;1]$ by:

\begin{align}S(x)&=\int_0^x \frac{t\ln t}{1+t^2}\,dt\\ &=\int_0^1 \frac{tx^2\ln(tx)}{1+t^2x^2}\,dt\\ \end{align}

\begin{align} \text{D}&=\int_0^1 \frac{x\ln x\ln(1+x)}{1+x^2}\,dx\\ &=\Big[S(x)\ln(1+x)\Big]_0^1-\int_0^1 \int_0^1\frac{tx^2\ln(tx)}{(1+t^2x^2)(1+x)}\,dt\,\,dx\\ &=\ln 2\int_0^1 \frac{x\ln x}{1+x^2}\,dx-\int_0^1 \int_0^1\frac{tx^2\ln t}{(1+t^2x^2)(1+x)}\,dt\,\,dx-\int_0^1 \int_0^1\frac{tx^2\ln x}{(1+t^2x^2)(1+x)}\,dt\,\,dx\\ &=\left(\int_0^1\frac{t\ln t\ln(1+t^2)}{2(1+t^2)}\,dt-\int_0^1\frac{\ln t\ln(1+t^2)}{2t}\,dt+\int_0^1\frac{\ln t\arctan t}{1+t^2}\,dt-\int_0^1\frac{(\ln 2)t\ln t}{1+t^2}\,dt\right)-\\ &\frac{1}{2}\int_0^1 \frac{\ln(1+x^2)\ln x}{1+x}\,dx+\ln 2\int_0^1 \frac{x\ln x}{1+x^2}\,dx\\ \end{align}

In the first, second, fourth, sixth integrals perform the change of variable $\displaystyle y=t^2$ (or $ \displaystyle y=x^2$),

\begin{align} \text{D}&=\frac{1}{8}\int_0^1\frac{\ln t\ln(1+t)}{1+t}\,dt-\frac{1}{8}\int_0^1\frac{\ln t\ln(1+t)}{t}\,dt+\int_0^1\frac{\ln t\arctan t}{1+t^2}\,dt-\frac12 \text{C}\\ &=\frac{1}{8}\int_0^1\frac{\ln t\ln(1+t)}{1+t}\,dt-\frac{1}{16}\Big[\ln^2 t\ln(1+t)\Big]_0^1+\frac{1}{16}\int_0^1 \frac{\ln^2 t}{1+t}\,dt+\int_0^1\frac{\ln t\arctan t}{1+t^2}\,dt-\frac12 \text{C}\\ &=\frac{1}{8}\int_0^1\frac{\ln t\ln(1+t)}{1+t}\,dt+\frac{1}{16}\int_0^1 \frac{\ln^2 t}{1+t}\,dt+\int_0^1\frac{\ln t\arctan t}{1+t^2}\,dt-\frac12 \text{C}\\ \end{align}

Define function $T$ on $[0;1]$ by:

\begin{align}T(x)&=\int_0^x \frac{\ln t}{1+t^2}\,dt\\ &=\int_0^1 \frac{x\ln(tx)}{1+t^2x^2}\,dt\\ \end{align}

Observe that,

\begin{align}T(0)&=0\\ T(1)`&=-\text{G} \end{align}

\begin{align}\text{E}&=\int_0^1\frac{\ln x\arctan x}{1+x^2}\,dx\\ &=\Big[T(x)\arctan x\Big]_0^1-\int_0^1\int_0^1 \frac{x\ln(tx)}{(1+x^2)(1+t^2x^2)}\,dt\,dx\\ &=-\frac{\text{G}\pi}{4}-\int_0^1\int_0^1 \frac{x\ln t}{(1+x^2)(1+t^2x^2)}\,dt\,dx-\int_0^1\int_0^1 \frac{x\ln x}{(1+x^2)(1+t^2x^2)}\,dt\,dx\\ &=-\frac{\text{G}\pi}{4}+\frac12\int_0^1 \frac{\ln t\ln\left(\frac{1+t^2}{2}\right)}{1-t^2}\,dt-E\\ \end{align}

Observe that for $t\in [0;1[$,

\begin{align}\frac{1}{1-t^2}=\frac{1}{1+t}+\frac{t}{1-t^2} \end{align}

Therefore,

\begin{align}E&=-\frac{\text{G}\pi}{4}-\frac{\ln 2}{2}\int_0^1 \frac{\ln t}{1-t^2}\,dt+\frac12\int_0^1 \frac{t\ln t\ln\left(1+t^2\right)}{1-t^2}\,dt+\frac{1}{2}\text{C}-\text{E}\end{align}

In the latter integral perform the change of variable $\displaystyle y=t^2$

\begin{align}E&=-\frac{\text{G}\pi}{4}-\frac{\ln 2}{2}\int_0^1 \frac{\ln t}{1-t^2}\,dt+\frac18\int_0^1 \frac{\ln t\ln\left(1+t\right)}{1-t}\,dt+\frac{1}{2}\text{C}-\text{E}\\ &=-\frac{\text{G}\pi}{4}-\frac{\ln 2}{2}\int_0^1 \frac{\ln t}{1-t^2}\,dt+\frac{\ln 2}{8}\int_0^1 \frac{\ln t}{1-t}\,dt+\frac18\int_0^1 \frac{\ln t\ln\left(\frac{1+t}{2}\right)}{1-t}\,dt+\\ &\frac{1}{2}\text{C}-\text{E} \end{align}

In the latter integral perform the change of variable $y=\dfrac{1-t}{1+t}$,

\begin{align}E&=-\frac{\text{G}\pi}{4}-\frac{\ln 2}{2}\int_0^1 \frac{\ln t}{1-t^2}\,dt+\frac{\ln 2}{8}\int_0^1 \frac{\ln t}{1-t}\,dt-\\ &\frac18\int_0^1\left(\frac{1}{t}-\frac{1}{1+t}\right)\ln\left(\frac{1-t}{1+t}\right)\ln\left(1+t\right)\,dt+\frac{1}{2}\text{C}-\text{E}\\ &=-\frac{\text{G}\pi}{4}-\frac{\ln 2}{2}\int_0^1 \frac{\ln t}{1-t^2}\,dt+\frac{\ln 2}{8}\int_0^1 \frac{\ln t}{1-t}\,dt+\\ &\frac18\int_0^1 \frac{\ln\left(\frac{1-t}{1+t}\right)\ln\left(1+t\right)}{1+t}\,dx+\frac18\int_0^1 \frac{\ln^2\left(1+t\right)}{t}\,dt-\\ &\frac18\int_0^1 \frac{\ln\left(1+t\right)\ln\left(1-t\right)}{t}\,dt+\frac{1}{2}\text{C}-\text{E}\\ \int_0^1 \frac{\ln^2\left(1+t\right)}{t}\,dt&=\Big[\ln t\ln^2(1+t)\Big]_0^1-2\int_0^1 \frac{\ln t\ln(1+t)}{1+t}\,dt\\ &=-2\int_0^1 \frac{\ln t\ln(1+t)}{1+t}\,dt\\ F&=\int_0^1 \frac{\ln(1+t)\ln(1-t) }{t}\,dt\\ &=\frac12 \left(\int_0^1 \frac{t\ln^2(1-t^2) }{t^2}\,dt-\int_0^1 \frac{\ln^2(1-t) }{t}\,dt-\int_0^1 \frac{\ln^2(1+t) }{t}\,dt\right)\\ \end{align}

In the first integral perform the change of variable $\displaystyle y=1-t^2$,

In the second integral perform the change of variable $\displaystyle y=1-t$,

\begin{align}F&=\frac12 \left(2\int_0^1 \frac{\ln t\ln(1+t) }{1+t}\,dt-\int_0^1 \frac{\ln^2 t }{1-t}\,dt+\frac{1}{2}\int_0^1 \frac{\ln^2 t }{1-t}\,dt\right)\\ &=\int_0^1 \frac{\ln t\ln(1+t) }{1+t}\,dt-\frac14\int_0^1 \frac{\ln^2 t }{1-t}\,dt\\ H&=\int_0^1 \frac{\ln\left(\frac{1-t}{1+t}\right)\ln\left(1+t\right)}{1+t}\,dt \end{align}

Perform the change of variable $y=\dfrac{1-t}{1+t}$,

\begin{align}H&=\int_0^1 \frac{\ln\left(\frac{2}{1+t}\right)\ln t}{1+t}\,dt\\ &=\ln 2\int_0^1 \frac{\ln t}{1+t}\,dt-\int_0^1 \frac{\ln t\ln(1+t)}{1+t}\,dt \end{align}

Therefore,

\begin{align}2E&=-\frac{\text{G}\pi}{4}-\frac{\ln 2}{2}\int_0^1 \frac{\ln t}{1-t^2}\,dt+\frac{\ln 2}{8}\int_0^1 \frac{\ln t}{1-t}\,dt+\\ &\frac{1}{8}\left( \ln 2\int_0^1 \frac{\ln t}{1+t}\,dt-\int_0^1 \frac{\ln t\ln(1+t)}{1+t}\,dt\right)-\frac14\int_0^1 \frac{\ln t\ln(1+t)}{1+t}\,dt-\\ &\frac18\left( \int_0^1 \frac{\ln t\ln(1+t) }{1+t}\,dt-\frac14\int_0^1 \frac{\ln^2 t }{1-t}\,dt\right)+\frac{1}{2}\text{C}\\ E&=\frac{\text{C}}{4}-\frac{\text{G}\pi}{8}-\frac{\ln 2}{8} \int_0^1\frac{\ln t}{1-t^2}\,dt+\frac{1}{64} \int_0^1\frac{\ln^2 t}{1-t}\,dt-\frac14\int_0^1 \frac{\ln t\ln(1+t)}{1+t}\,dt \\ \end{align}

Therefore,

\begin{align}D&=\frac{1}{16} \int_0^1 \frac{\ln^2 t}{1+t}\,dt+\frac{1}{64} \int_0^1 \frac{\ln^2 t}{1-t}\,dt-\frac{1}{8} \int_0^1 \frac{\ln(1+t)\ln t}{1+t}\,dt-\\ &\frac{\ln 2}{8} \int_0^1 \frac{\ln t}{1-t^2}\,dt -\frac{\text{C}}{4}-\frac{\text{G}\pi} {8}\\ &=\frac{1}{64} \int_0^1 \frac{\ln^2 t}{1-t}\,dt-\frac{3}{16} \int_0^1 \frac{\ln^2 t}{1+t}\,dt-\frac{1}{8} \int_0^1 \frac{\ln(1+t)\ln t}{1+t}\,dt-\\ &\frac{\ln 2}{8} \int_0^1 \frac{\ln t}{1-t^2}\,dt-\frac{3\ln 2}{16}\int_0^1 \frac{\ln t}{1+t}\,dt\\ B&=\frac12\Big((A+B)-(A-B)\Big)\\ &=\frac{\ln^3 2}{12}+\frac{\text{G}\pi}{4}-\frac{1}{64}\int_0^1 \frac{\ln^2 t}{1-t}\,dt+\int_0^1 \frac{\ln t\ln(1+t)}{1+t}\,dt-\\ &\frac{5}{16}\int_0^1 \frac{\ln^2 t}{1+t}\,dt-\frac{5\ln 2}{16}\int_0^1 \frac{\ln t}{1+t}\,dt+\frac{\ln 2}{8}\int_0^1 \frac{\ln t}{1-t^2}\,dt\\ \end{align}

Since, for $t\neq 1$,

\begin{align}\frac{1}{1+t}&=\frac{1}{1-t}-\frac{2t}{1-t^2}\\ \frac{1}{1-t^2}&=\frac{1}{1-t}-\frac{t}{1-t^2} \end{align}

then,

\begin{align}\text{B}&=\frac{\ln^3 2}{12}+\frac{\text{G}\pi}{4}-\frac{21}{64}\int_0^1 \frac{\ln^2 t}{1-t}\,dt+\int_0^1 \frac{\ln t\ln(1+t)}{1+t}\,dt-\\ &\frac{3\ln 2}{16}\int_0^1 \frac{\ln t}{1-t}\,dt+\frac{\ln 2}{2}\int_0^1 \frac{t\ln t}{1-t^2}\,dt+\frac{5}{8}\int_0^1 \frac{t\ln^2 t}{1-t^2}\,dt\\ \end{align}

In the two latter integrals perform the change of variable $\displaystyle y=t^2$,

\begin{align}\text{B}&=\frac{\ln^3 2}{12}+\frac{\text{G}\pi}{4}-\frac{1}{4}\int_0^1 \frac{\ln^2 t}{1-t}\,dt+\int_0^1 \frac{\ln t\ln(1+t)}{1+t}\,dt-\\ &\frac{\ln 2}{16}\int_0^1 \frac{\ln t}{1-t}\,dt\\ U&=\int_0^1\frac{\ln(1+t)\ln t}{1+t}\,dt\\ W&=\int_0^1\frac{\ln^2\left(\frac{t}{1+t}\right)}{1+t}\,dt\\ \end{align}

Perform the change of variable $y=\dfrac{t}{1+t}$,

\begin{align} W&=\int_0^{\frac{1}{2}}\frac{\ln^2 t}{1-t}\,dt\\ &=\int_0^1\frac{\ln^2 x}{1-t}\,dt-\int_{\frac{1}{2}}^1\frac{\ln^2 t}{1-t}\,dt\\ \end{align}

In the latter integral perform the change of variable $y=\dfrac{1-t}{t}$

\begin{align} W&=\int_0^1\frac{\ln^2 t}{1-t}\,dt-\int_0^1\frac{\ln^2(1+t)}{t(1+t)}\,dt\\ &=\int_0^1\frac{\ln^2 t}{1-t}\,dt+\int_0^1\frac{\ln^2(1+t)}{1+t}\,dt-\int_0^1\frac{\ln^2(1+t)}{t}\,dt\\ &=\int_0^1\frac{\ln^2 t}{1-t}\,dt+\int_0^1\frac{\ln^2(1+t)}{1+t}\,dt-\Big[\ln t\ln^2(1+t)\Big]_0^1+2\int_0^1 \frac{\ln x\ln(1+t)}{1+t}\,dt\\ &=\int_0^1\frac{\ln^2 t}{1-t}\,dt+\int_0^1\frac{\ln^2(1+t)}{1+t}\,dt+2U\\ \end{align}

On the other hand,

\begin{align} W&=\int_0^1\frac{\left(\ln t-\ln(1+t)\right)^2}{1+t}\,dt\\ &=\int_0^1\frac{\ln^2 t}{1+t}\,dt+\int_0^1\frac{\ln^2(1+t)}{1+t}\,dx-2U\\ \end{align}

Therefore,

\begin{align} U&=\frac{1}{4}\left(\int_0^1\frac{\ln^2 t}{1+t}\,dt-\int_0^1\frac{\ln^2 t}{1-t}\,dt\right)\\ &=-\frac{1}{4}\int_0^1\frac{2t\ln^2 t}{1-t^2}\,dt \end{align}

Perform the change of variable $\displaystyle y=t^2$,

\begin{align} U&=-\frac{1}{16}\int_0^1\frac{\ln^2 t}{1-t}\,dt\\ \end{align}

Therefore,

\begin{align}\text{B}&=\frac{\ln^3 2}{12}+\frac{\text{G}\pi}{4}-\frac{5}{16}\int_0^1 \frac{\ln^2 t}{1-t}\,dt-\frac{\ln 2}{16}\int_0^1 \frac{\ln t}{1-t}\,dt\\ &=\frac{\ln^3 2}{12}+\frac{\text{G}\pi}{4}-\frac{5}{16}\times 2\zeta(3)-\frac{\ln 2}{16}\times -\frac{\pi^2}{6}\\ &=\boxed{\frac{1}{12}\ln^3 2+\frac{1}{4}\text{G}\pi-\frac{5}{8}\zeta(3)+\frac{1}{96}\pi^2\ln 2} \end{align}

Answer 3

I hope you won't mind my attempt to the indefinite integral using polylogarithms. NOT AN ANSWER

I re-wrote $\log^2(1+x^2)$ as $$\log^2(1+ix)(1-ix)=\log^2(1+ix) + 2\log(1+ix)\log(1-ix) + \log^2(1-ix).$$ Therefore you can write \begin{eqnarray} \mathcal I &=& \int\frac{\log^2(1+x^2)}{1+x}dx=\\ &=& \underbrace{\int\frac{\log^2(1+ix)}{1+x}dx}_{\mathcal I_1} + 2\underbrace{\int\frac{\log(1+ix)\log(1-ix)}{1+x}dx}_{\mathcal I_2}+\\ & &+\underbrace{\int\frac{\log^2(1-ix)}{1+x}dx}_{\mathcal I_3}\tag{*}\label{3} \end{eqnarray} I first concentrated on the integral $$\mathcal I_1 = \int \frac{\log^2(1+ix)}{1+x}dx$$ for which I used the change of variables $$\omega = \frac{x+1}{2} -i \frac{x+1}{2},$$ that gives $$ x = (1+i)\omega -1,$$ $$1+ix = (1-i)(\omega + 1),$$ and $$dx = (1+i)d\omega.$$ So we get \begin{eqnarray} \mathcal I_1 &=& \int \frac{\left[\log(1-i)+\log(1+\omega)\right]^2}{\omega}d\omega=\\ &=&\log^2(1-i)\log \omega +2\log(1-i) \text{Li}_2(-\omega) +\underbrace{\int\frac{\text{Li}_1^2(-\omega)}{\omega}d\omega}_{\mathcal A(\omega)}. \end{eqnarray} Integrating by parts $\mathcal A$ yields \begin{eqnarray} \mathcal A(\omega) &=& \text{Li}_1^2(-\omega)\log(-\omega) + 2\int\frac{\text{Li}_1(-\omega)\log(-\omega)}{1+\omega}d\omega=\\ &=&\text{Li}_1^2(-\omega)\log(-\omega) + 2\int \text{Li}_1(-\omega)d\text{Li}_2(1+\omega)=\\ &=&\text{Li}_1^2(-\omega)\log(-\omega)+2\text{Li}_1(-\omega)\text{Li}_2(1+\omega) + 2\int \frac{\text{Li}_2(1+\omega)}{1+\omega}d\omega=\\ &=&\text{Li}_1^2(-\omega)\log(-\omega)+2\text{Li}_1(-\omega)\text{Li}_2(1+\omega) + \text{Li}_3(1+\omega). \end{eqnarray} Thus we get \begin{eqnarray} \mathcal I_1 &=&\log^2(1-i)\log \omega +2\log(1-i) \text{Li}_2(-\omega) +\\ &&+\text{Li}_1^2(-\omega)\log(-\omega)+2\text{Li}_1(-\omega)\text{Li}_2(1+\omega) + \text{Li}_3(1+\omega) \end{eqnarray}

Now, using the same change of variable in $\mathcal I_3$ we get \begin{eqnarray} \mathcal I_3 &=& \int \frac{\left[\log(1+i)+\log(1-i\omega)\right]^2}{\omega}d\omega=\\ &=&\log^2(1+i)\log \omega +2\log(1+i) \text{Li}_2(i\omega) +\underbrace{\int\frac{\text{Li}_1^2(i\omega)}{\omega}d\omega}_{\mathcal B(\omega)}. \end{eqnarray} Observe that $$\mathcal B(\omega) = i\mathcal A(-i\omega).$$ Thus we can use the results already obtained to get \begin{eqnarray} \mathcal I_3 &=& \log^2(1+i)\log \omega +2\log(1+i) \text{Li}_2(i\omega) +\\ &&+i\text{Li}_1^2(i\omega)\log(i\omega)+2i\text{Li}_1(i\omega)\text{Li}_2(1-i\omega) + i\text{Li}_3(1-i\omega) \end{eqnarray}

Again the same change on variables yields, for $\mathcal I_2$, \begin{eqnarray} \mathcal I_2 &=& \int\frac{[\log(1-i)+\log(1+\omega)][\log(1+i)+\log(1-i\omega)}{\omega}d\omega=\\ &=& \log 2 \log \omega + \log(i-1)\text{Li}_2(i\omega)+\\ &&+\log(i+1)\text{Li}_2(-\omega)+\underbrace{\int\frac{\log(1-i\omega)\log(1+\omega)}{\omega}d\omega}_{\mathcal C}. \end{eqnarray} $\mathcal C$ is the trickiest part. Haven't completed it yet.

Answer 4

Here is a solution similar to FDP's, by trying to build a relation with a similar integral we have: $$I=\int _0^1\frac{x\ln \left(1-x\right)\ln \left(1+x^2\right)}{1+x^2}\:dx,\:J=\int _0^1\frac{x\ln \left(1+x\right)\ln \left(1+x^2\right)}{1+x^2}\:dx$$

$$I+J=\int _0^1\frac{x\ln \left(1-x^2\right)\ln \left(1+x^2\right)}{1+x^2}\:dx$$ $$=\frac{1}{2}\int _0^1\frac{\ln \left(1-x\right)\ln \left(1+x\right)}{1+x}\:dx$$ $$I+J=\frac{1}{16}\zeta \left(3\right)-\frac{1}{4}\ln \left(2\right)\zeta \left(2\right)+\frac{1}{6}\ln ^3\left(2\right)$$ That last integral can be computed easily if one considers the algebraic identity $ab=\frac{1}{4}\left(a+b\right)^2-\frac{1}{4}\left(a-b\right)^2$.

---

$$I-J=\int _0^1\frac{x\ln \left(\frac{1-x}{1+x}\right)\ln \left(1+x^2\right)}{1+x^2}\:dx$$ $$=\int _0^1\frac{\ln \left(x\right)\ln \left(1+x^2\right)}{1+x}\:dx+\ln \left(2\right)\int _0^1\frac{\ln \left(x\right)}{1+x}\:dx-2\underbrace{\int _0^1\frac{\ln \left(x\right)\ln \left(1+x\right)}{1+x}\:dx}_{N}$$ $$-\int _0^1\frac{x\ln \left(x\right)\ln \left(1+x^2\right)}{1+x^2}\:dx-\ln \left(2\right)\int _0^1\frac{x\ln \left(x\right)}{1+x^2}\:dx+2\underbrace{\int _0^1\frac{x\ln \left(x\right)\ln \left(1+x\right)}{1+x^2}\:dx}_{K}$$ $$=\int _0^1\frac{\ln \left(x\right)\ln \left(1+x^2\right)}{1+x}\:dx-\frac{3}{8}\ln \left(2\right)\zeta \left(2\right)-\frac{9}{4}\int _0^1\frac{\ln \left(x\right)\ln \left(1+x\right)}{1+x}\:dx$$ $$+2\int _0^1\frac{x\ln \left(x\right)\ln \left(1+x\right)}{1+x^2}\:dx$$ $$=\int _0^1\frac{\ln \left(x\right)\ln \left(1+x^2\right)}{1+x}\:dx-\frac{3}{16}\zeta \left(3\right)$$ $$=-2\int _0^1\frac{x\ln \left(x\right)\ln \left(1+x\right)}{1+x^2}\:dx-\int _0^1\frac{\ln \left(1+x\right)\ln \left(1+x^2\right)}{x}dx-\frac{3}{16}\zeta \left(3\right)$$ $$=\frac{9}{32}\zeta \left(3\right)-\frac{3}{8}\ln \left(2\right)\zeta \left(2\right)+\frac{1}{2}\sum _{k=1}^{\infty }\frac{\left(-1\right)^kH_{2k}}{k^2}-\frac{1}{2}\sum _{k=1}^{\infty }\frac{\left(-1\right)^kH_k}{k^2}$$ $$=\frac{9}{32}\zeta \left(3\right)-\frac{3}{8}\ln \left(2\right)\zeta \left(2\right)+\frac{23}{32}\zeta \left(3\right)-\frac{\pi }{2}G+\frac{5}{16}\zeta \left(3\right)$$ $$I-J=\frac{21}{16}\zeta \left(3\right)-\frac{3}{8}\ln \left(2\right)\zeta \left(2\right)-\frac{\pi }{2}G$$ The integral $N$ can be computed quite simply by considering the substitution $x=\frac{1}{1+x}$.

As for the integral $K$ can be found calculated in a similar fashion in the book (Almost) Impossible Integrals, Sums, and Series page $\#98$.

---

We have: \begin{alignat*}{4} I & {}+{} & J & {}={} \frac{1}{16}\zeta \left(3\right)-\frac{1}{4}\ln \left(2\right)\zeta \left(2\right)+\frac{1}{6}\ln ^3\left(2\right) \\ I & {}-{} & J & {}={} \frac{21}{16}\zeta \left(3\right)-\frac{3}{8}\ln \left(2\right)\zeta \left(2\right)-\frac{\pi }{2}G \\ \end{alignat*}

---

So we conclude that: $$I=\int _0^1\frac{x\ln \left(1-x\right)\ln \left(1+x^2\right)}{1+x^2}\:dx=\frac{11}{16}\zeta \left(3\right)-\frac{5}{16}\ln \left(2\right)\zeta \left(2\right)-\frac{\pi }{4}G+\frac{1}{12}\ln ^3\left(2\right)$$ $$J=\int _0^1\frac{x\ln \left(1+x\right)\ln \left(1+x^2\right)}{1+x^2}\:dx=-\frac{5}{8}\zeta \left(3\right)+\frac{1}{16}\ln \left(2\right)\zeta \left(2\right)+\frac{\pi }{4}G+\frac{1}{12}\ln ^3\left(2\right)$$